Learning Objectives

In this lecture, we will

• Continue our discussion of numerical and visual summaries of data

  • We discuss contingency tables and bar plots for summarizing categorical data. Textbook section 2.2.1.
  • We see how to use R to compute numerical summaries and visualizations for categorical data.

Summaries of Categorical Data Video

• Please watch this video on your own time.

A Note on Categorical Variables in R

• Often, a categorical variable is called a factor, and each category is called a level.

• For example, consider letter grades such as we assign at the University. This is a factor with 11 levels: A, A-, B+, B, B-, C+, C, C-, D+, D, and F.

• Note that here we know all of the possible outcomes (levels) a priori.

Creating a Factor in R

Here is an example of creating a factor in R:

my_grades <- factor(
  c(rep("A",4),rep("B",6),rep("B-",4),rep("C",8),rep("C-",2),
                      rep("D",2),rep("F",3)),
                    levels=c("A","A-","B+","B","B-","C+","C","C-","D+","D","F")
  )

Recall the table Function

table(my_grades)

## my_grades
##  A A- B+  B B- C+  C C- D+  D  F 
##  4  0  0  6  4  0  8  2  0  2  3

• The table function returns the count of how many times each level of a factor appears in the data. This is sometimes called a frequency table.

• A table such as the one we just obtained is a typical way to summarize a single categorical variable.

Bar Plots

A barplot is the visual analog of a frequency table.

grades_df <- tibble(my_grades=my_grades)
gf_bar(~my_grades,data=grades_df)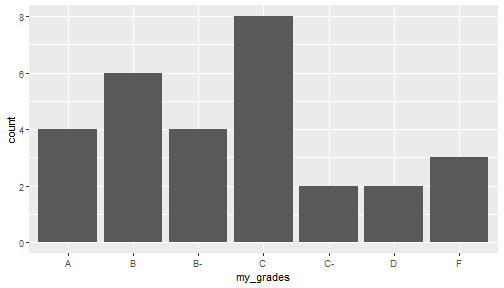

Summarizing Data for Two Categorical Variables

Scatterplots provide a way to summarize together two numerical variables, methods for summarizing together two categorical variables include:

• Contingency tables

• Proportion tables

• Stacked or side-by-side bar plots

• Mosaic plots

We will explain each of these tools and illustrate how to obtain them in R. We will work with the loans_dat data set. This data set represents thousands of loans made through the Lending Club platform, which is a platform that allows individuals to lend to other individuals.

Contingency Tables

Contingency tables display the number of times a particular combination of variable outcomes occurs.

• For example, we construct a contingency table for the variables homeownership (ownership status of the applicant's residence) and application_type (type of application: either individual or joint):

with(loans_dat,addmargins(table(application_type,homeownership)))

##                 homeownership
## application_type MORTGAGE   OWN  RENT   Sum
##       individual     3839  1170  3496  8505
##       joint           950   183   362  1495
##       Sum            4789  1353  3858 10000

• If we create a barplot for homeownership, we will see bars corresponding to the first three values in the last row of our table. Similarly, a barplot for application_type will show bars corresponding to the first two values in the last column of our table.

Bar Plots for loans_dat

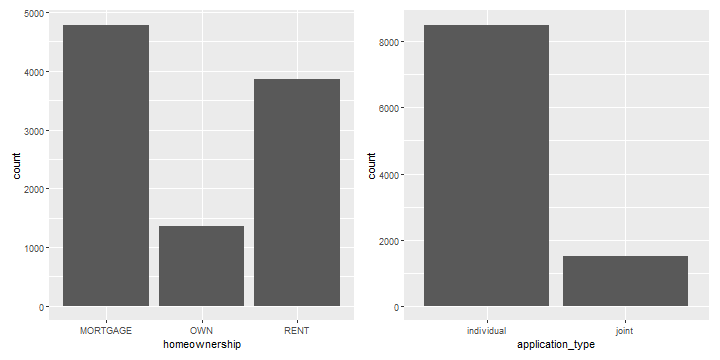
##                 homeownership
## application_type MORTGAGE   OWN  RENT   Sum
##       individual     3839  1170  3496  8505
##       joint           950   183   362  1495
##       Sum            4789  1353  3858 10000

Proportion Tables

At times, it is useful to compute proportions instead of counts.

• A proportion table displays the same essential information as a contingency table except we divide entries by either the row sums (row proportion table) or the column sum (column proportion table).

• For example, if we divide each entry in the first row of the previous table by 8505, and divide each entry in the second row by 1495, we obtain

(c(3839,1170,3496) / 8505)

## [1] 0.4513815 0.1375661 0.4110523

(c(950, 183, 362) / 1495)

## [1] 0.6354515 0.1224080 0.2421405

• This gives us our values for a row proportion table.

Proportion Tables Example

• Row proportion table

with(loans_dat,addmargins(prop.table(table(application_type,homeownership),
                                     margin=1)))

##                 homeownership
## application_type  MORTGAGE       OWN      RENT       Sum
##       individual 0.4513815 0.1375661 0.4110523 1.0000000
##       joint      0.6354515 0.1224080 0.2421405 1.0000000
##       Sum        1.0868330 0.2599742 0.6531928 2.0000000

• Column proportion table

with(loans_dat,addmargins(prop.table(table(application_type,homeownership),
                                     margin=2)))

##                 homeownership
## application_type  MORTGAGE       OWN      RENT       Sum
##       individual 0.8016287 0.8647450 0.9061690 2.5725427
##       joint      0.1983713 0.1352550 0.0938310 0.4274573
##       Sum        1.0000000 1.0000000 1.0000000 3.0000000

Stacked and Side-By-Side Barplots

p1 <- gf_bar(~homeownership,data=loans_dat,fill=~application_type) + 
  ggtitle("Stacked")
p2 <- gf_bar(~homeownership,data=loans_dat,fill=~application_type,
             position = position_dodge()) + ggtitle("Side-By-Side")
p1 + p2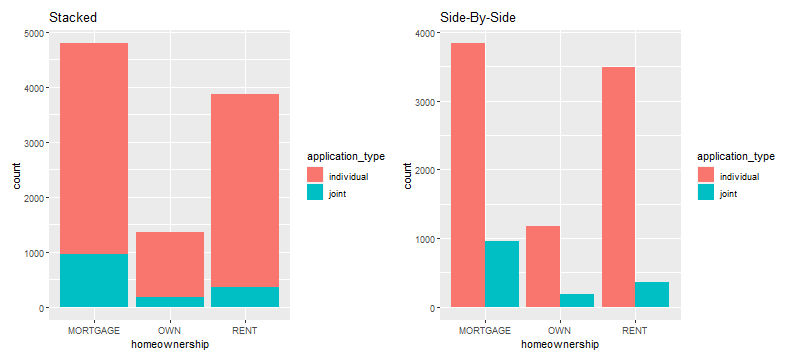

Standardized Stacked Bar Plot

Stacked bar plots can be used to contruct a visualization of a proportion table.

• For example, the following stacked bar plot displays our column proportion table as a plot:

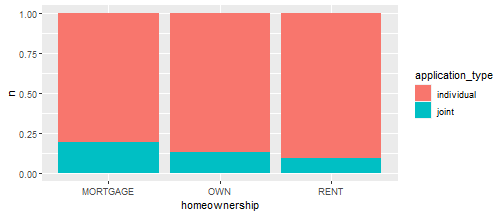
##                 homeownership
## application_type  MORTGAGE       OWN      RENT       Sum
##       individual 0.8016287 0.8647450 0.9061690 2.5725427
##       joint      0.1983713 0.1352550 0.0938310 0.4274573
##       Sum        1.0000000 1.0000000 1.0000000 3.0000000

Mosaic Plots

A mosiac plot is a visualization that corresponds to contingency tables. They can be one-variable of multi-variable.

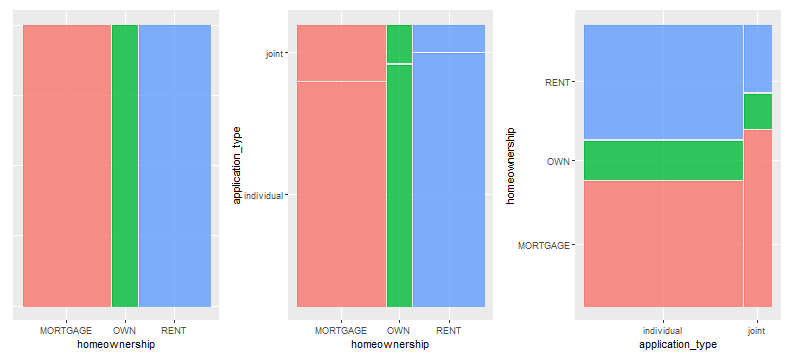
Grouped Numerical Data

• Grouped numerical data arises when we want to study the distribution of a numerical variable across two or more distinguishing groups.

• In other words, we are looking for association between two variables where one variable is numerical (typically viewed as the response variable) and the other is categorical (typically viewed as the explanatory variable).

• For example, consider out possum data set again.

head(possum,5)

## # A tibble: 5 x 8
##    site pop   sex     age head_l skull_w total_l tail_l
##   <int> <fct> <fct> <int>  <dbl>   <dbl>   <dbl>  <dbl>
## 1     1 Vic   m         8   94.1    60.4    89     36  
## 2     1 Vic   f         6   92.5    57.6    91.5   36.5
## 3     1 Vic   f         6   94      60      95.5   39  
## 4     1 Vic   f         6   93.2    57.1    92     38  
## 5     1 Vic   f         2   91.5    56.3    85.5   36

• We could ask, is there a difference in the distribution of possum tail length between female and male possums?

Grouped Summaries

We can compute grouped numerical summaries:

possum %>% group_by(sex) %>% summarise(mean_tail_l=mean(tail_l),
                                        median_tail_l=median(tail_l),
                                        tail_l_var=var(tail_l),
                                        sd_tail_l=sd(tail_l))

## # A tibble: 2 x 5
##   sex   mean_tail_l median_tail_l tail_l_var sd_tail_l
##   <fct>       <dbl>         <dbl>      <dbl>     <dbl>
## 1 f            37.1          37.5       3.35      1.83
## 2 m            36.9          36.5       4.23      2.06

Grouped plots

We can also create grouped plots:

p1 <- gf_boxplot(tail_l~sex,data=possum,color=~sex,binwidth=2)
p2 <- gf_histogram(~tail_l | sex,data=possum,fill=~sex,binwidth=2)
p1 + p2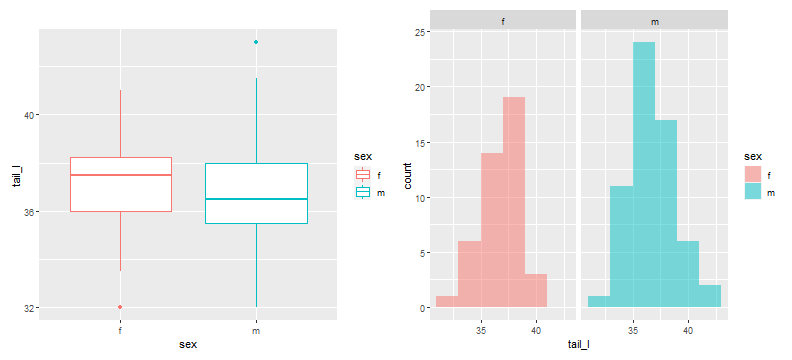

R Tips: the Tidyverse

In order to work with data, compute summaries, and obtain visualizations, we are employing the tidyverse family of R packages. This includes

• dplyr for working with and summarizing data

• ggplot2 for graphics and visualizations

• readr for reading data into R

• etc.

• The tidyverse utilizes the principle of tidy data for facilitating analyses.

Tidy Data

Visualizations in R

Reflection

In this lecture, we covered the topics of

• Graphical and numerical summaries for categorical data

• We discussed contigency tables and bar plot

• We introduced the notion of grouped data and grouped summaries

For Next Time

In the next lecture, we will begin our discussion of probability which forms the foundation of statistics. In preparation, you are encouraged to watch the included video.