Lecture 6Random VariablesJMGMATH 204Thursday, September 161 / 29

Learning Objectives

In this lecture, we will

Examine the most important concepts related to our study of random variables.

2 / 29

Learning Objectives

In this lecture, we will

Examine the most important concepts related to our study of random variables.
Recall from the last lecture that we introduced the notion of a random variable, that is, something that assigns a numerical value to events from a random process.

2 / 29

Learning Objectives

In this lecture, we will

Examine the most important concepts related to our study of random variables.
Recall from the last lecture that we introduced the notion of a random variable, that is, something that assigns a numerical value to events from a random process.
We typically denote random variables by capital letters at the end of the alphabet such as $X$ , $Y$ , or $Z$ .

2 / 29

Learning Objectives

In this lecture, we will

Examine the most important concepts related to our study of random variables.
Recall from the last lecture that we introduced the notion of a random variable, that is, something that assigns a numerical value to events from a random process.
We typically denote random variables by capital letters at the end of the alphabet such as $X$ , $Y$ , or $Z$ .
Our primary goal is to study methods that allow us to better understand the distribution of a random variable.

2 / 29

Learning Objectives

In this lecture, we will

Examine the most important concepts related to our study of random variables.
Recall from the last lecture that we introduced the notion of a random variable, that is, something that assigns a numerical value to events from a random process.
We typically denote random variables by capital letters at the end of the alphabet such as $X$ , $Y$ , or $Z$ .
Our primary goal is to study methods that allow us to better understand the distribution of a random variable.
Specifically, we will cover expectation, variance, discrete and continuous distributions, and some common random variables and their distributions. See textbook sections 3.4, 3.5, 4.1, 4.2, and 4.3.

2 / 29

Random Variable DistributionsIf a random variable has only a very small number of outcomes, then we can simply list its distribution. 
3 / 29

Random Variable Distributions

If a random variable has only a very small number of outcomes, then we can simply list its distribution.
For example, reconsider the process of rolling two six-sided dice. Let $X$ be the random variable that records the sum of the values shown by the two dice. Then the distribution for $X$ is

Dice sum	X=2	X=3	X=4	X=5	X=6	X=7	X=8	X=9	X=10	X=11	X=12
Probability	1/36	2/36	3/36	4/36	5/36	6/36	5/36	4/36	3/36	2/36	1/36

3 / 29

Random Variable Distributions

If a random variable has only a very small number of outcomes, then we can simply list its distribution.
For example, reconsider the process of rolling two six-sided dice. Let $X$ be the random variable that records the sum of the values shown by the two dice. Then the distribution for $X$ is

Dice sum	X=2	X=3	X=4	X=5	X=6	X=7	X=8	X=9	X=10	X=11	X=12
Probability	1/36	2/36	3/36	4/36	5/36	6/36	5/36	4/36	3/36	2/36	1/36

We can compute probability values associated with $X$ such as

$P (X = 3) = \frac{2}{36} = \frac{1}{18}$

$P (X <= 5) = \frac{1}{36} + \frac{2}{36} + \frac{3}{36} + \frac{4}{36} = \frac{10}{36} = \frac{5}{18}$

3 / 29

Tossing a CoinConsider the random process of tossing a coin where the probability of landing heads is a number pp. Let XX be the random variable that counts the number of heads after a single toss. 
4 / 29

Tossing a Coin

Consider the random process of tossing a coin where the probability of landing heads is a number $p$ . Let $X$ be the random variable that counts the number of heads after a single toss.
Construct the probability distribution for $X$ . Note that the only possible outcomes for $X$ is 0 or 1.

4 / 29

Tossing a Coin

Consider the random process of tossing a coin where the probability of landing heads is a number $p$ . Let $X$ be the random variable that counts the number of heads after a single toss.
Construct the probability distribution for $X$ . Note that the only possible outcomes for $X$ is 0 or 1.
Obviously $P (X = 1) = p$ .

4 / 29

Tossing a Coin

Consider the random process of tossing a coin where the probability of landing heads is a number $p$ . Let $X$ be the random variable that counts the number of heads after a single toss.
Construct the probability distribution for $X$ . Note that the only possible outcomes for $X$ is 0 or 1.
Obviously $P (X = 1) = p$ .
By the complement rule, we must have $P (X = 0) = 1 - p$ . Therefore,

Num Heads	X=0	X=1
Probability	1-p	p

4 / 29

Summaries for Random Variable DistributionsIn cases where it is not easy to completely write down the probability distribution for a random variable, it is useful to be able to characterize the distribution. 
5 / 29

Summaries for Random Variable Distributions

In cases where it is not easy to completely write down the probability distribution for a random variable, it is useful to be able to characterize the distribution.
The two most common characteristics we consider for the distribution of a random variable are its expectation or expected value, and its variance.

5 / 29

Summaries for Random Variable Distributions

In cases where it is not easy to completely write down the probability distribution for a random variable, it is useful to be able to characterize the distribution.
The two most common characteristics we consider for the distribution of a random variable are its expectation or expected value, and its variance.
We will discuss expectation first.

5 / 29

Discrete Vs. Continuous Random VariablesBefore we define the expectation of a random variable, it is helpful to distinguish two types of random variables. 
6 / 29

Discrete Vs. Continuous Random Variables

Before we define the expectation of a random variable, it is helpful to distinguish two types of random variables.
A random variable $X$ is called discrete if its outcomes form a discrete set.
A set is discrete if it can be labeled by the whole numbers 1, 2, 3, ...

6 / 29

Discrete Vs. Continuous Random Variables

Before we define the expectation of a random variable, it is helpful to distinguish two types of random variables.
A random variable $X$ is called discrete if its outcomes form a discrete set.
A set is discrete if it can be labeled by the whole numbers 1, 2, 3, ...
For example, the random variable that adds the values after a roll of two six-sided dice is a discrete random variable. Additionally, the random variable that counts the number of heads after tossing a coin 10 times is a discrete random variable.

6 / 29

Discrete Vs. Continuous Random Variables

Before we define the expectation of a random variable, it is helpful to distinguish two types of random variables.
A random variable $X$ is called discrete if its outcomes form a discrete set.
A set is discrete if it can be labeled by the whole numbers 1, 2, 3, ...
For example, the random variable that adds the values after a roll of two six-sided dice is a discrete random variable. Additionally, the random variable that counts the number of heads after tossing a coin 10 times is a discrete random variable.
Later we will describe continuous random variables. However, it's important to note that there are random variables that are neither discrete or continuous.

6 / 29

ExpectationExpectation, or the expected value of a random variable XX measures the average outcome for XX. We typically denote the expectation of XX by E(X)E(X), or sometimes by μμ.  
7 / 29

Expectation

Expectation, or the expected value of a random variable $X$ measures the average outcome for $X$ . We typically denote the expectation of $X$ by $E (X)$ , or sometimes by $μ$ .
The expected value of a discrete random variable $X$ is the sum of the products of its outcomes times its probability values.

7 / 29

Expectation

Expectation, or the expected value of a random variable $X$ measures the average outcome for $X$ . We typically denote the expectation of $X$ by $E (X)$ , or sometimes by $μ$ .
The expected value of a discrete random variable $X$ is the sum of the products of its outcomes times its probability values.
Mathematically,

$E (X) = x_{1} P (X = x_{1}) + x_{2} P (X = x_{2}) + \dots + x_{n} P (X = x_{n})$

7 / 29

Expectation

Expectation, or the expected value of a random variable $X$ measures the average outcome for $X$ . We typically denote the expectation of $X$ by $E (X)$ , or sometimes by $μ$ .
The expected value of a discrete random variable $X$ is the sum of the products of its outcomes times its probability values.
Mathematically,

$E (X) = x_{1} P (X = x_{1}) + x_{2} P (X = x_{2}) + \dots + x_{n} P (X = x_{n})$

For example, if $X$ is the random variable that adds the values after a roll of two six-sided dice, then

$\begin{aligned} E (X) & = 2 \frac{1}{36} + 3 \frac{2}{36} + 4 \frac{3}{36} + 5 \frac{4}{36} + 6 \frac{5}{36} \\ + 7 \frac{6}{36} + 8 \frac{5}{36} + 9 \frac{4}{36} + 10 \frac{3}{36} + 11 \frac{2}{36} + 12 \frac{1}{36} \\ = \frac{245}{36} \approx 6.8 \end{aligned}$

7 / 29

Considering Data

The following shows the first few rows from data collected after repeatedly tossing two dice 5,000 times and adding up their values after each toss:

## # A tibble: 6 x 3
##   die_1 die_2   sum
##   <int> <int> <int>
## 1     6     2    12
## 2     2     4     4
## 3     6     5    12
## 4     2     4     4
## 5     2     6     4
## 6     6     4    12

8 / 29

Considering Data

The following shows the first few rows from data collected after repeatedly tossing two dice 5,000 times and adding up their values after each toss:

## # A tibble: 6 x 3
##   die_1 die_2   sum
##   <int> <int> <int>
## 1     6     2    12
## 2     2     4     4
## 3     6     5    12
## 4     2     4     4
## 5     2     6     4
## 6     6     4    12

Let's compute the mean for the sum variable:

## [1] 7.0548

8 / 29

Considering Data

The following shows the first few rows from data collected after repeatedly tossing two dice 5,000 times and adding up their values after each toss:

## # A tibble: 6 x 3
##   die_1 die_2   sum
##   <int> <int> <int>
## 1     6     2    12
## 2     2     4     4
## 3     6     5    12
## 4     2     4     4
## 5     2     6     4
## 6     6     4    12

Let's compute the mean for the sum variable:

## [1] 7.0548

The point is that expected value is to random variables what the mean is to data.

8 / 29

Considering Data

The following shows the first few rows from data collected after repeatedly tossing two dice 5,000 times and adding up their values after each toss:

## # A tibble: 6 x 3
##   die_1 die_2   sum
##   <int> <int> <int>
## 1     6     2    12
## 2     2     4     4
## 3     6     5    12
## 4     2     4     4
## 5     2     6     4
## 6     6     4    12

Let's compute the mean for the sum variable:

## [1] 7.0548

The point is that expected value is to random variables what the mean is to data.
That is, if we take a very large number of samples from a random variable and compute the sample mean, then this will give us an accurate (but not exact) estimate for the expected value.

8 / 29

Another Expectation ExampleSuppose we let XX be the random variable that counts the number of heads after a single toss of a coin with probability of getting heads pp. 
9 / 29

Another Expectation Example

Suppose we let $X$ be the random variable that counts the number of heads after a single toss of a coin with probability of getting heads $p$ .
Then,

$E (X) = 1 \cdot p + 0 \cdot (1 - p) = p$

9 / 29

Another Expectation Example

Suppose we let $X$ be the random variable that counts the number of heads after a single toss of a coin with probability of getting heads $p$ .
Then,

$E (X) = 1 \cdot p + 0 \cdot (1 - p) = p$

If our coin is fair, then $p = \frac{1}{2}$ and $E (X) = \frac{1}{2}$ .

9 / 29

Another Expectation Example

Suppose we let $X$ be the random variable that counts the number of heads after a single toss of a coin with probability of getting heads $p$ .
Then,

$E (X) = 1 \cdot p + 0 \cdot (1 - p) = p$

If our coin is fair, then $p = \frac{1}{2}$ and $E (X) = \frac{1}{2}$ .
Here's the mean of 1,000 samples from this random variable (number of heads for a fair coin):

## [1] 0.527

9 / 29

Basic Properties of ExpectationThe expected value satisfies some important properties, among the most important are:
10 / 29

Basic Properties of Expectation

The expected value satisfies some important properties, among the most important are:
If we multiply a random variable $X$ by a number $a$ , and then add another number $b$ , then we can compute the expected value in either of two ways and get the same answer. Mathematically,

$E (a X + b) = a E (X) + b .$

10 / 29

Basic Properties of Expectation

The expected value satisfies some important properties, among the most important are:
If we multiply a random variable $X$ by a number $a$ , and then add another number $b$ , then we can compute the expected value in either of two ways and get the same answer. Mathematically,

$E (a X + b) = a E (X) + b .$

If we have two random variables $X$ and $Y$ , and we multiply them each by a different number and add the result, then we can compute the expected value in either of two ways and get the same answer. Mathematically,

$E (a X + b Y) = a E (X) + b E (Y)$

10 / 29

Basic Properties of Expectation

The expected value satisfies some important properties, among the most important are:
If we multiply a random variable $X$ by a number $a$ , and then add another number $b$ , then we can compute the expected value in either of two ways and get the same answer. Mathematically,

$E (a X + b) = a E (X) + b .$

If we have two random variables $X$ and $Y$ , and we multiply them each by a different number and add the result, then we can compute the expected value in either of two ways and get the same answer. Mathematically,

$E (a X + b Y) = a E (X) + b E (Y)$

The previous result extends to any number of random variables. In particular,

$E (X_{1} + X_{2} + \dots + X_{n}) = E (X_{1}) + E (X_{2}) + \dots + E (X_{n})$

10 / 29

Examples Working with ExpectationWe will take a pause from the slides to work out some examples together. 
11 / 29

Variance of a Random VariableWe have seen that expected value is to random variables what the mean is to data. What is the analog of the sample variance of data for a random variable? 
12 / 29

Variance of a Random Variable

We have seen that expected value is to random variables what the mean is to data. What is the analog of the sample variance of data for a random variable?
The answer is the variance of a random variable. If $X$ is a random variable and $μ$ is its expected value, then the variance of $X$ is

$Var (X) = E ((X - μ)^{2})$

The standard deviation of a random variable $X$ is the square root of its variance $sd (X) = \sqrt{Var (X)}$ .

12 / 29

Variance of a Random Variable

We have seen that expected value is to random variables what the mean is to data. What is the analog of the sample variance of data for a random variable?
The answer is the variance of a random variable. If $X$ is a random variable and $μ$ is its expected value, then the variance of $X$ is

$Var (X) = E ((X - μ)^{2})$

The standard deviation of a random variable $X$ is the square root of its variance $sd (X) = \sqrt{Var (X)}$ .
It is helpful to know that if $a$ and $b$ are numbers and if $X$ is a random variable, then

$Var (a X + b) = a^{2} Var (X)$

12 / 29

Considering Data for VarianceYou can take it on faith that if XX is the random variable that returns the number of heads after a single toss of a fair coin, then Var(X)=14=0.25Var(X)=14=0.25. Let's see how this compares with the sample variance of some data:
13 / 29

Considering Data for Variance

You can take it on faith that if $X$ is the random variable that returns the number of heads after a single toss of a fair coin, then $Var (X) = \frac{1}{4} = 0.25$ . Let's see how this compares with the sample variance of some data:
The sample variance after 1,000 sample tosses is

## [1] 0.2502142

13 / 29

Examples Working with VarianceWe will take a pause from the slides to work out some examples together. 
14 / 29

Famous Distributions and Their PropertiesNow that we have covered the principal concepts regarding random variables, we introduce some famous types of random variables and describe their distributions. 
15 / 29

Famous Distributions and Their Properties

Now that we have covered the principal concepts regarding random variables, we introduce some famous types of random variables and describe their distributions.
We begin with some famous discrete distributions.

15 / 29

Famous Distributions and Their Properties

Now that we have covered the principal concepts regarding random variables, we introduce some famous types of random variables and describe their distributions.
We begin with some famous discrete distributions.
Bernoulli, Geometric, and Binomial

15 / 29

Famous Distributions and Their Properties

Now that we have covered the principal concepts regarding random variables, we introduce some famous types of random variables and describe their distributions.
We begin with some famous discrete distributions.
Bernoulli, Geometric, and Binomial
Then we discuss continuous random variables and the most famous continuous distribution, the normal distribution.

15 / 29

Bernoulli Random Variable

A Bernoulli random variable (section 4.2.1) is a random variable $X$ corresponding to a random process with exactly two possible outcomes typically labeled "success" and "failure", a so-called Bernoulli trial. We define $X$ by counting the number of successes after a single trial so that $X = 1$ (for a success) and $X = 0$ for failure.

16 / 29

Bernoulli Random Variable

If $p$ is the probability of success, then the probability distribution of $X$ is

Num Successes	X=0	X=1
Probability	1-p	p

16 / 29

Bernoulli Random Variable

If $p$ is the probability of success, then the probability distribution of $X$ is

Num Successes	X=0	X=1
Probability	1-p	p

If $X$ is a Bernoulli random variable, then

$μ = E (X) = p, and σ^{2} = Var (X) = p (1 - p)$

16 / 29

Bernoulli Random Variable

If $p$ is the probability of success, then the probability distribution of $X$ is

Num Successes	X=0	X=1
Probability	1-p	p

If $X$ is a Bernoulli random variable, then

$μ = E (X) = p, and σ^{2} = Var (X) = p (1 - p)$

Note that the flip of a coin can be modeled by a Bernoulli random variable if we think of tossing heads as a success and if the probability of tossing heads is $p$ .

16 / 29

Bernoulli ExamplesWe take a break from the slides to work out some examples related to Bernoulli random variables. 
17 / 29

The Geometric Distribution

The geometric distribution is used to describe how many trials it takes to observe a success.

18 / 29

The Geometric Distribution

The geometric distribution is used to describe how many trials it takes to observe a success.

Suppose we conduct a sequence of $n$ independent Bernoulli trials with probability of success $p$ . What is the probability that it takes $n$ trials to obtain the first success?

18 / 29

The Geometric Distribution

The geometric distribution is used to describe how many trials it takes to observe a success.

Suppose we conduct a sequence of $n$ independent Bernoulli trials with probability of success $p$ . What is the probability that it takes $n$ trials to obtain the first success?
Let $A$ be the event that the first success occurs on the $n$ -th trial. Then $A$ can be realized as the event $A = F_{1} and F_{2} and \dots and F_{n - 1} and S_{1}$ , where and $F$ corresponds to a failure event and an $S$ corresponds to a success event. Since there are all independent, we have

$P (A) = P (F_{1}) P (F_{2}) \dots P (F_{n - 1}) P (S_{1}) = (1 - p)^{n - 1} p$

18 / 29

The Geometric Distribution

The geometric distribution is used to describe how many trials it takes to observe a success.

Suppose we conduct a sequence of $n$ independent Bernoulli trials with probability of success $p$ . What is the probability that it takes $n$ trials to obtain the first success?
Let $A$ be the event that the first success occurs on the $n$ -th trial. Then $A$ can be realized as the event $A = F_{1} and F_{2} and \dots and F_{n - 1} and S_{1}$ , where and $F$ corresponds to a failure event and an $S$ corresponds to a success event. Since there are all independent, we have

$P (A) = P (F_{1}) P (F_{2}) \dots P (F_{n - 1}) P (S_{1}) = (1 - p)^{n - 1} p$

If $X$ is a random variable with a geometric distribution, then

$μ = E (X) = \frac{1}{p}, and σ^{2} = Var (X) = \frac{1 - p}{p^{2}}$

18 / 29

Geometric Distribution ExamplesWe take a break from the slides to work out some examples related to Geometric random variables.
19 / 29

The Binomial DistributionThe binomial distribution is used to describe the number of successes in a fixed number of trials. This is different from the geometric distribution, which describes the number of trials we must wait before we observe a success. 
20 / 29

The Binomial Distribution

The binomial distribution is used to describe the number of successes in a fixed number of trials. This is different from the geometric distribution, which describes the number of trials we must wait before we observe a success.
For a binomial distribution,

20 / 29

The Binomial Distribution

The binomial distribution is used to describe the number of successes in a fixed number of trials. This is different from the geometric distribution, which describes the number of trials we must wait before we observe a success.
For a binomial distribution,
- The number of trials, $n$ , is fixed.

20 / 29

The Binomial Distribution

The binomial distribution is used to describe the number of successes in a fixed number of trials. This is different from the geometric distribution, which describes the number of trials we must wait before we observe a success.
For a binomial distribution,
- The number of trials, $n$ , is fixed.
- The trials are independent.

20 / 29

The Binomial Distribution

The binomial distribution is used to describe the number of successes in a fixed number of trials. This is different from the geometric distribution, which describes the number of trials we must wait before we observe a success.
For a binomial distribution,
- The number of trials, $n$ , is fixed.
- The trials are independent.
- Each trial outcome can be classified as a success or failure.

20 / 29

The Binomial Distribution

The binomial distribution is used to describe the number of successes in a fixed number of trials. This is different from the geometric distribution, which describes the number of trials we must wait before we observe a success.
For a binomial distribution,
- The number of trials, $n$ , is fixed.
- The trials are independent.
- Each trial outcome can be classified as a success or failure.
- The probability of a success, $p$ , is the same for each trial.

20 / 29

Mathematics of the Binomial Distribution

Suppose the probability of a single trial being a success is $p$ . Then the probability of observing exactly $k$ successes in $n$ independent trials is given by

$\begin{aligned} (\binom{n}{k}) p^{k} (1 - p)^{n - k} & = \frac{n!}{k! (n - k)!} p^{k} (1 - p)^{n - k} \end{aligned}$

21 / 29

Mathematics of the Binomial Distribution

Suppose the probability of a single trial being a success is $p$ . Then the probability of observing exactly $k$ successes in $n$ independent trials is given by

$\begin{aligned} (\binom{n}{k}) p^{k} (1 - p)^{n - k} & = \frac{n!}{k! (n - k)!} p^{k} (1 - p)^{n - k} \end{aligned}$

The mean, variance, and standard deviation of the number of observed successes are

$\begin{aligned} μ & = n p & σ^{2} & = n p (1 - p) & σ & = \sqrt{n p (1 - p)} \end{aligned}$

21 / 29

Binomial Distribution ExamplesWe take a break from the slides to work out some examples related to Binomial random variables.
22 / 29

Binomial Distribution Examples

We take a break from the slides to work out some examples related to Binomial random variables.
This video is also recommended:

22 / 29

Continuous DistributionsEach of the Bernoulli, Geometric, and Binomial distributions are discrete. 
23 / 29

Continuous DistributionsEach of the Bernoulli, Geometric, and Binomial distributions are discrete. 
We will also be interested in continuous random variables. 
23 / 29

Continuous Distributions

Each of the Bernoulli, Geometric, and Binomial distributions are discrete.
We will also be interested in continuous random variables.
Continuous random variables are tricky to define precisely. Roughly, a random variable $X$ is a continuous random variable if its outcomes are continuous numerical values.

23 / 29

Continuous Distributions

Each of the Bernoulli, Geometric, and Binomial distributions are discrete.
We will also be interested in continuous random variables.
Continuous random variables are tricky to define precisely. Roughly, a random variable $X$ is a continuous random variable if its outcomes are continuous numerical values.
Consider for example a random variable $X$ whose outcomes can be any real number in the interval $[0, 1]$ and with each outcome equally likely. Such a random variable is said to follow a uniform distribution on $[0, 1]$ .

23 / 29

Continuous Distributions

Each of the Bernoulli, Geometric, and Binomial distributions are discrete.
We will also be interested in continuous random variables.
Continuous random variables are tricky to define precisely. Roughly, a random variable $X$ is a continuous random variable if its outcomes are continuous numerical values.
Consider for example a random variable $X$ whose outcomes can be any real number in the interval $[0, 1]$ and with each outcome equally likely. Such a random variable is said to follow a uniform distribution on $[0, 1]$ .
If $x$ is any real number in $[0, 1]$ , then $P (X = x) = 0$ . However, if $a, b$ are any two real numbers in $[0, 1]$ with $a \leq b$ , then $P (a \leq X \leq b) = b - a$ .

23 / 29

Continuous Distributions

Each of the Bernoulli, Geometric, and Binomial distributions are discrete.
We will also be interested in continuous random variables.
Continuous random variables are tricky to define precisely. Roughly, a random variable $X$ is a continuous random variable if its outcomes are continuous numerical values.
Consider for example a random variable $X$ whose outcomes can be any real number in the interval $[0, 1]$ and with each outcome equally likely. Such a random variable is said to follow a uniform distribution on $[0, 1]$ .
If $x$ is any real number in $[0, 1]$ , then $P (X = x) = 0$ . However, if $a, b$ are any two real numbers in $[0, 1]$ with $a \leq b$ , then $P (a \leq X \leq b) = b - a$ .
The quantity $P (a \leq X \leq b)$ is interpreted as the probability of randomly selecting any real number in $[0, 1]$ that lies between $a$ and $b$ .

23 / 29

Samples from a Uniform Distribution

The following plot shows a histogram of 10,000 random samples from a uniform distribution on $[0, 1]$ :

24 / 29

Samples from a Uniform Distribution

The following plot shows a histogram of 10,000 random samples from a uniform distribution on $[0, 1]$ :

24 / 29

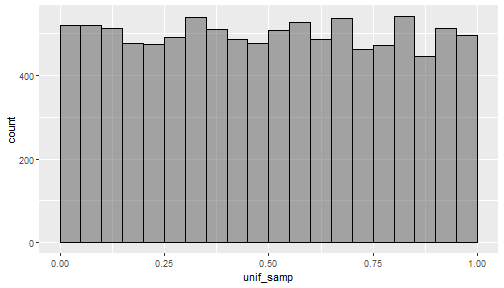
Samples from a Uniform Distribution

The following plot shows a histogram of 10,000 random samples from a uniform distribution on $[0, 1]$ :

If you had to guess, what do you think are the expected value and standard deviation for a uniform random variable on $[0, 1]$ ?

24 / 29

Uniform Distribution: Density

The following plot shows the probability density function for a uniformly distributed random variable on $[0, 1]$ :

25 / 29

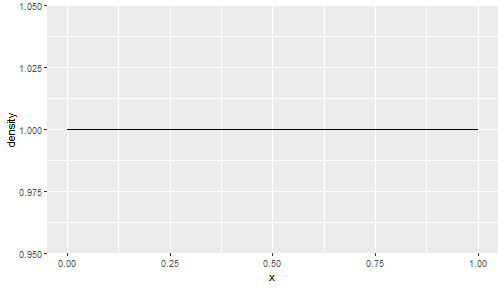
Uniform Distribution: Density

The following plot shows the probability density function for a uniformly distributed random variable on $[0, 1]$ :

Pick two values $a$ and $b$ that lie within $[0, 1]$ . Then the area that falls under the density function and between the lines $x = a$ and $x = b$ corresponds to the probability that a random variable $X$ uniform on $[0, 1]$ takes values between $a$ and $b$ .

25 / 29

Are Under a Density Function

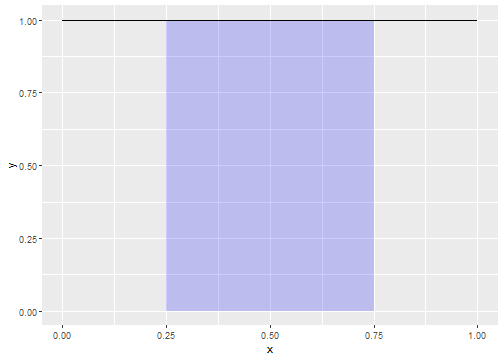
The following shaded rectangle shows the area under the density function for a uniform distribution on $[0, 1]$ between 0.25 and 0.75. This area represents the probability that a value for a random variable $X$ uniformly distribution on $[0, 1]$ falls between 0.25 and 0.75. Thus, $P (0.25 \leq X \leq 0.75) = 0.75 - 0.25 = 0.5$ .

26 / 29

General Continuous DistributionsHopefully, the last few slides provide intuition for the following facts:
27 / 29

General Continuous Distributions

Hopefully, the last few slides provide intuition for the following facts:
- If $X$ is a random variable, and there is a continuous function $f$ such that $P (a \leq X \leq b) = area under graph of f$ between $a$ and $b$ , then $X$ is a continuous random variable with probability density function $f$ .

27 / 29

General Continuous Distributions

Hopefully, the last few slides provide intuition for the following facts:
- If $X$ is a random variable, and there is a continuous function $f$ such that $P (a \leq X \leq b) = area under graph of f$ between $a$ and $b$ , then $X$ is a continuous random variable with probability density function $f$ .
Note that for any density function $f$ , we require that the total area under the graph of $f$ is 1.

27 / 29

The Normal DistributionPerhaps the most famous and most important continuous distribution is the so-called normal distribution. This will be the topic of our next lecture. 
28 / 29

The Normal DistributionPerhaps the most famous and most important continuous distribution is the so-called normal distribution. This will be the topic of our next lecture. 
To prepare for the next lecture, please watch the following video:


28 / 29

R Commands for DistributionsWe now show how you can use R to work with the distributions we have introduced so far. 
29 / 29

R Commands for Distributions

We now show how you can use R to work with the distributions we have introduced so far.
Here is what you need to know:
- Each distribution has a short hand name such binom, geom, unif, or norm.

29 / 29

R Commands for Distributions

We now show how you can use R to work with the distributions we have introduced so far.
Here is what you need to know:
- Each distribution has a short hand name such binom, geom, unif, or norm.
- Each distribution has four functions associated with it. For example, the four functions associated with binom are
- rbinom - draws random samples from a binomial random variable

29 / 29

R Commands for Distributions

We now show how you can use R to work with the distributions we have introduced so far.
Here is what you need to know:
- Each distribution has a short hand name such binom, geom, unif, or norm.
- Each distribution has four functions associated with it. For example, the four functions associated with binom are
- rbinom - draws random samples from a binomial random variable
- dbinom - implements the probability function for a binomial random variable

29 / 29

R Commands for Distributions

We now show how you can use R to work with the distributions we have introduced so far.
Here is what you need to know:
- Each distribution has a short hand name such binom, geom, unif, or norm.
- Each distribution has four functions associated with it. For example, the four functions associated with binom are
- rbinom - draws random samples from a binomial random variable
- dbinom - implements the probability function for a binomial random variable
- pbinom & qbinom which implement the distribution function and quantile function respectively for a binomial random variable. We have not really discussed the concepts related to these functions at this point.

29 / 29

R Commands for Distributions

We now show how you can use R to work with the distributions we have introduced so far.
Here is what you need to know:
- Each distribution has a short hand name such binom, geom, unif, or norm.
- Each distribution has four functions associated with it. For example, the four functions associated with binom are
- rbinom - draws random samples from a binomial random variable
- dbinom - implements the probability function for a binomial random variable
- pbinom & qbinom which implement the distribution function and quantile function respectively for a binomial random variable. We have not really discussed the concepts related to these functions at this point.
Let's go to R together and see how these all work.

29 / 29

↑, ←, Pg Up, k	Go to previous slide
↓, →, Pg Dn, Space, j	Go to next slide
Home	Go to first slide
End	Go to last slide
Number + Return	Go to specific slide
b / m / f	Toggle blackout / mirrored / fullscreen mode
c	Clone slideshow
p	Toggle presenter mode
t	Restart the presentation timer
?, h	Toggle this help