Lecture 7
The Normal Distribution
JMG
MATH 204
Tuesday, September 21
Learning Objectives
In this lecture, we will
- Study the normal distribution and learn how to compute probability values for a random variable that follows a normal distribution.
Learning Objectives
In this lecture, we will
Study the normal distribution and learn how to compute probability values for a random variable that follows a normal distribution.
The normal distribution is a continuous distribution. We will discuss the so-called normal curve which is the probability density function for a normal distribution.
Learning Objectives
In this lecture, we will
Study the normal distribution and learn how to compute probability values for a random variable that follows a normal distribution.
The normal distribution is a continuous distribution. We will discuss the so-called normal curve which is the probability density function for a normal distribution.
We will also learn about the expected value and variance for a normal random variable.
Learning Objectives
In this lecture, we will
Study the normal distribution and learn how to compute probability values for a random variable that follows a normal distribution.
The normal distribution is a continuous distribution. We will discuss the so-called normal curve which is the probability density function for a normal distribution.
We will also learn about the expected value and variance for a normal random variable.
This lecture corresponds to section 4.1 in the textbook, and you are encouraged to watch the lecture video included in the next slide.
Normal Distribution Video
Samples from a Normal Distribution
- The following histogram shows 5,000 random samples from a normal random variable:
tibble(x=rnorm(5000,66,3.5)) %>% gf_histogram(~x,color="black")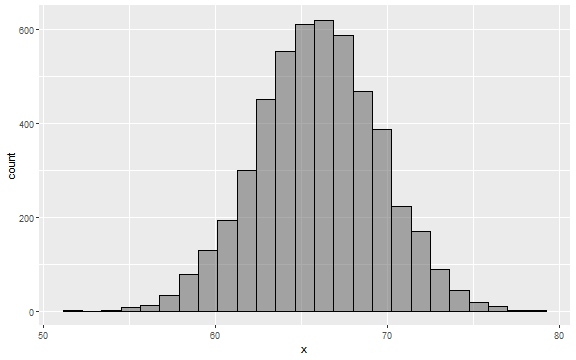
Normal Histogram Discussion
- Think of the histogram on the previous slide as showing sample data for measurements of human heights in inches.
Normal Histogram Discussion
Think of the histogram on the previous slide as showing sample data for measurements of human heights in inches.
What are the key features of the histogram?
Normal Histogram Discussion
Think of the histogram on the previous slide as showing sample data for measurements of human heights in inches.
What are the key features of the histogram?
It is unimodal, highly symmetric, and centered at the mean.
Normal Histogram Discussion
Think of the histogram on the previous slide as showing sample data for measurements of human heights in inches.
What are the key features of the histogram?
It is unimodal, highly symmetric, and centered at the mean.
Do you think that such data could reasonably correspond to measurements of human heights in inches?
Normal Histogram Discussion
Think of the histogram on the previous slide as showing sample data for measurements of human heights in inches.
What are the key features of the histogram?
It is unimodal, highly symmetric, and centered at the mean.
Do you think that such data could reasonably correspond to measurements of human heights in inches?
Do you think it is reasonable to treat measurements of human heights in inches as a continuous variable?
Normal Distribution Facts
Many random variables are nearly normal, but none are exactly normal. Thus the normal distribution, while not perfect for any single problem, is very useful for a variety of problems. We will use it in data exploration and to solve important problems in statistics.
Normal Distribution Facts
Many random variables are nearly normal, but none are exactly normal. Thus the normal distribution, while not perfect for any single problem, is very useful for a variety of problems. We will use it in data exploration and to solve important problems in statistics.
- Let's spend some time to develop some intuition for how the normal distribution is often used in practice.
Normal Distribution Facts
Many random variables are nearly normal, but none are exactly normal. Thus the normal distribution, while not perfect for any single problem, is very useful for a variety of problems. We will use it in data exploration and to solve important problems in statistics.
Let's spend some time to develop some intuition for how the normal distribution is often used in practice.
We start by generating some data that is not necessarily normally distributed.
Sampling a Mean
- We are going to play a game. We proceed as follows:
Sampling a Mean
We are going to play a game. We proceed as follows:
1) Sample 15 values from a binomial random variable with n=25 and p=0.5. You can think of this as doing 15 rounds of an experiment where each time we flip a fair coin 25 times and count the number of heads that we obtain.
Sampling a Mean
We are going to play a game. We proceed as follows:
1) Sample 15 values from a binomial random variable with n=25 and p=0.5. You can think of this as doing 15 rounds of an experiment where each time we flip a fair coin 25 times and count the number of heads that we obtain.
2) We compute and record the mean of the 15 values obtained in step 1.
Sampling a Mean
We are going to play a game. We proceed as follows:
1) Sample 15 values from a binomial random variable with n=25 and p=0.5. You can think of this as doing 15 rounds of an experiment where each time we flip a fair coin 25 times and count the number of heads that we obtain.
2) We compute and record the mean of the 15 values obtained in step 1.
3) We repeat steps 1 & 2 a very large number of times, say 2,500.
Sampling a Mean
We are going to play a game. We proceed as follows:
1) Sample 15 values from a binomial random variable with n=25 and p=0.5. You can think of this as doing 15 rounds of an experiment where each time we flip a fair coin 25 times and count the number of heads that we obtain.
2) We compute and record the mean of the 15 values obtained in step 1.
3) We repeat steps 1 & 2 a very large number of times, say 2,500.
Here is the first few rows of a data frame that contains the data we acquire by playing our game.
## # A tibble: 6 x 1## means## <dbl>## 1 12.5## 2 12.5## 3 13.1## 4 12.2## 5 12 ## 6 12.3Plotting Our Data
- Here is a histogram of the data we obtained from the game described on the previous slide:
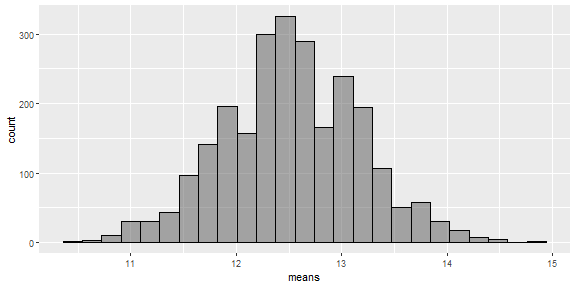
Plotting Our Data
- Here is a histogram of the data we obtained from the game described on the previous slide:

- The mean of our data is 12.523. What is the expected value of a binomial random variable with n=25 and p=0.5?
A Normal Density Function
- The following plot shows a normal density curve:
gf_dist("norm")
Center and Shape of a Normal Curve
- There are two parameters called μ (mean) and σ (sd) that determine the center and shape, respectively of a normal curve. For example,:
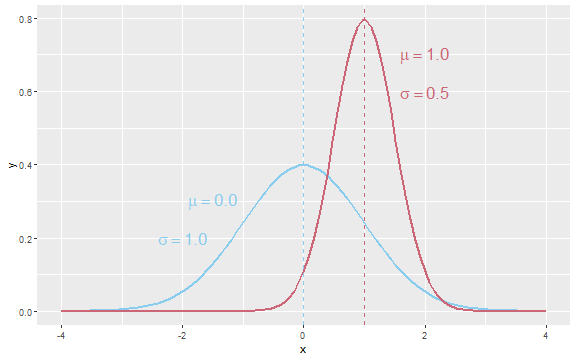
Going Back to Data
- Recall that to obtain our data, we drew 15 independent samples from a binomial distribution with n=25 and p=0.5, took the sample mean, and repeated this many times. The following plot shows the histogram of our data (with density instead of count on the y-axis) and overlays a particular normal density curve.
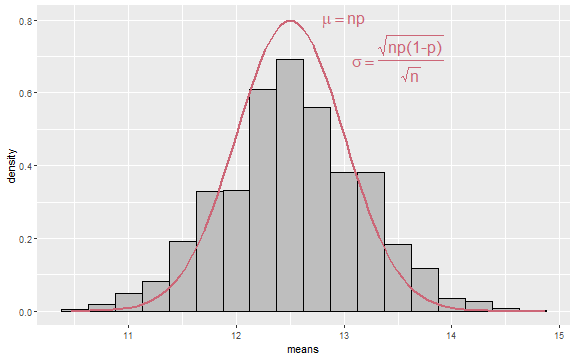
Sampling Distribution of the Mean
- We can think of the sample mean as a random variable. The sample mean inputs sample data of a fixed size from a population and returns the mean of the data.
Sampling Distribution of the Mean
We can think of the sample mean as a random variable. The sample mean inputs sample data of a fixed size from a population and returns the mean of the data.
The point is that the sample mean will vary as the sample varies.
Sampling Distribution of the Mean
We can think of the sample mean as a random variable. The sample mean inputs sample data of a fixed size from a population and returns the mean of the data.
The point is that the sample mean will vary as the sample varies.
What the last slide shows us is that, at least in the particular example, the distribution of the sample mean (viewed as a random variable) is very close to a random variable that is normally distributed.
Sampling Distribution of the Mean
We can think of the sample mean as a random variable. The sample mean inputs sample data of a fixed size from a population and returns the mean of the data.
The point is that the sample mean will vary as the sample varies.
What the last slide shows us is that, at least in the particular example, the distribution of the sample mean (viewed as a random variable) is very close to a random variable that is normally distributed.
In general, we call the distribution of the sample mean (viewed as a random variable), the sampling distribution of the mean. It is a general fact that the sampling distribution of the mean (for independent samples) is always very close to a normal distribution, regardless of the type of distribution used to sample the data for which the sample mean is computed.
Sampling Distribution of the Mean
We can think of the sample mean as a random variable. The sample mean inputs sample data of a fixed size from a population and returns the mean of the data.
The point is that the sample mean will vary as the sample varies.
What the last slide shows us is that, at least in the particular example, the distribution of the sample mean (viewed as a random variable) is very close to a random variable that is normally distributed.
In general, we call the distribution of the sample mean (viewed as a random variable), the sampling distribution of the mean. It is a general fact that the sampling distribution of the mean (for independent samples) is always very close to a normal distribution, regardless of the type of distribution used to sample the data for which the sample mean is computed.
This is the reason why the normal distribution plays such a central role in statistics.
Notation for Normal Random Variables
- If X is a normal random variable with expected value μ=E(X) and standard deviation σ=√Var(X), then we write X∼N(μ,σ).
Notation for Normal Random Variables
If X is a normal random variable with expected value μ=E(X) and standard deviation σ=√Var(X), then we write X∼N(μ,σ).
For example, if we have a normal random variable X with expected value 12.5 and standard deviation 0.5, then we write X∼N(μ=12.5,σ=0.5).
Notation for Normal Random Variables
If X is a normal random variable with expected value μ=E(X) and standard deviation σ=√Var(X), then we write X∼N(μ,σ).
For example, if we have a normal random variable X with expected value 12.5 and standard deviation 0.5, then we write X∼N(μ=12.5,σ=0.5).
We call a random variable Z that satisfies Z∼N(μ=0,σ=1) a standard normal variable and we call the normal distribution with μ=0 and σ=1 the standard normal distribution.
Notation for Normal Random Variables
If X is a normal random variable with expected value μ=E(X) and standard deviation σ=√Var(X), then we write X∼N(μ,σ).
For example, if we have a normal random variable X with expected value 12.5 and standard deviation 0.5, then we write X∼N(μ=12.5,σ=0.5).
We call a random variable Z that satisfies Z∼N(μ=0,σ=1) a standard normal variable and we call the normal distribution with μ=0 and σ=1 the standard normal distribution.
Our next goal is to see how to use the normal density function to compute probability values for a random variable that follows a normal distribution.
Standardizing with Z-scores
- Let X∼N(μ,σ) be a normal random variable.
Standardizing with Z-scores
Let X∼N(μ,σ) be a normal random variable.
Define a new random variable Z=X−μσ. We can compute the expectation and variance of Z as follows:
Standardizing with Z-scores
Let X∼N(μ,σ) be a normal random variable.
Define a new random variable Z=X−μσ. We can compute the expectation and variance of Z as follows:
E(Z)=E(X−μσ)=1σE(X−μ)=1σ(E(X)−μ)=1σ(μ−μ)=0
Standardizing with Z-scores
Let X∼N(μ,σ) be a normal random variable.
Define a new random variable Z=X−μσ. We can compute the expectation and variance of Z as follows:
E(Z)=E(X−μσ)=1σE(X−μ)=1σ(E(X)−μ)=1σ(μ−μ)=0
Var(Z)=Var(X−μσ)=1σ2Var(X−μ)=1σ2Var(X)=σ2σ2=1
Standardizing with Z-scores
Let X∼N(μ,σ) be a normal random variable.
Define a new random variable Z=X−μσ. We can compute the expectation and variance of Z as follows:
E(Z)=E(X−μσ)=1σE(X−μ)=1σ(E(X)−μ)=1σ(μ−μ)=0
Var(Z)=Var(X−μσ)=1σ2Var(X−μ)=1σ2Var(X)=σ2σ2=1
- So, if X∼N(μ,σ), then Z∼N(0,1), where Z=X−μσ.
Standardizing with Z-scores
Let X∼N(μ,σ) be a normal random variable.
Define a new random variable Z=X−μσ. We can compute the expectation and variance of Z as follows:
E(Z)=E(X−μσ)=1σE(X−μ)=1σ(E(X)−μ)=1σ(μ−μ)=0
Var(Z)=Var(X−μσ)=1σ2Var(X−μ)=1σ2Var(X)=σ2σ2=1
- So, if X∼N(μ,σ), then Z∼N(0,1), where Z=X−μσ.
- This is all a little abstract, so let's think about standardizing from a different perspective.
Standardizing Data
- The following table shows the mean and standard deviation for total scores on the SAT and ACT exams:
| SAT | ACT | |
|---|---|---|
| Mean | 1100 | 21 |
| SD | 200 | 6 |
Standardizing Data
- The following table shows the mean and standard deviation for total scores on the SAT and ACT exams:
| SAT | ACT | |
|---|---|---|
| Mean | 1100 | 21 |
| SD | 200 | 6 |
- Suppose we know that one person scored 1300 on the SAT and another person scored 24 on the ACT. Who had the better exam score? The numbers alone can not be compared. But their standardized Z-scores can.
Standardizing Data
- The following table shows the mean and standard deviation for total scores on the SAT and ACT exams:
| SAT | ACT | |
|---|---|---|
| Mean | 1100 | 21 |
| SD | 200 | 6 |
- Suppose we know that one person scored 1300 on the SAT and another person scored 24 on the ACT. Who had the better exam score? The numbers alone can not be compared. But their standardized Z-scores can.
person 1 Z-score=1300−1100200=1, person 2 Z-score=24−216=12
Standardizing Data
- The following table shows the mean and standard deviation for total scores on the SAT and ACT exams:
| SAT | ACT | |
|---|---|---|
| Mean | 1100 | 21 |
| SD | 200 | 6 |
- Suppose we know that one person scored 1300 on the SAT and another person scored 24 on the ACT. Who had the better exam score? The numbers alone can not be compared. But their standardized Z-scores can.
person 1 Z-score=1300−1100200=1, person 2 Z-score=24−216=12
- So we conclude that person 1 had the better exam score.
Standardizing Data
- The following table shows the mean and standard deviation for total scores on the SAT and ACT exams:
| SAT | ACT | |
|---|---|---|
| Mean | 1100 | 21 |
| SD | 200 | 6 |
- Suppose we know that one person scored 1300 on the SAT and another person scored 24 on the ACT. Who had the better exam score? The numbers alone can not be compared. But their standardized Z-scores can.
person 1 Z-score=1300−1100200=1, person 2 Z-score=24−216=12
So we conclude that person 1 had the better exam score.
Note that observations above the mean have a positive Z-score while observations below the mean have a negative Z-score.
Probability for Normal R.V.'s
- The first thing to know is that the total area under a normal density function is equal to 1. This is true regardless of the values for μ and σ. Thus, the shaded area shown below is 1:
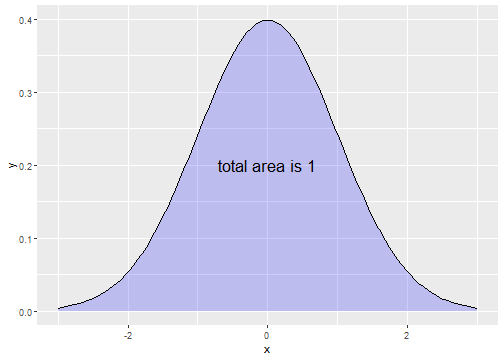
Tail Areas
- Suppose that X∼N(μ,σ), how do we find an area such as one of the ones shown below. That is, how do we find the area under one of the tails of a normal density function?
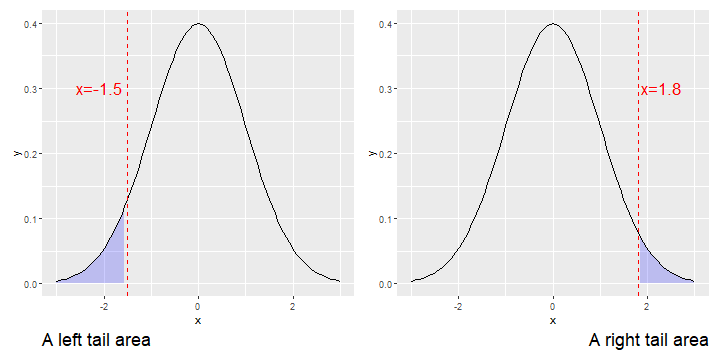
Interpreting Tail Areas
- In the last slide, the shaded area on the left represents the probability of an outcome being less than or equal to -1.5.
Interpreting Tail Areas
In the last slide, the shaded area on the left represents the probability of an outcome being less than or equal to -1.5.
In the last slide, the shaded area on the right represents the probability of an outcome being greater than or equal to 1.8.
Interpreting Tail Areas
In the last slide, the shaded area on the left represents the probability of an outcome being less than or equal to -1.5.
In the last slide, the shaded area on the right represents the probability of an outcome being greater than or equal to 1.8.
We will use Z-scores and the standard normal distribution to compute such areas.
Interpreting Tail Areas
In the last slide, the shaded area on the left represents the probability of an outcome being less than or equal to -1.5.
In the last slide, the shaded area on the right represents the probability of an outcome being greater than or equal to 1.8.
We will use Z-scores and the standard normal distribution to compute such areas.
We proceed by first learning to compute tail areas under the standard normal density curve which corresponds to a random variable Z∼N(μ=0,σ=1).
Standard Normal Tail Areas
- We spell out the steps for computing tail areas under the standard normal density function.
Standard Normal Tail Areas
We spell out the steps for computing tail areas under the standard normal density function.
- First, draw a picture of the tail area you want to compute.
Standard Normal Tail Areas
We spell out the steps for computing tail areas under the standard normal density function.
First, draw a picture of the tail area you want to compute.
Decide if it's a left tail area or a right tail area.
Standard Normal Tail Areas
We spell out the steps for computing tail areas under the standard normal density function.
First, draw a picture of the tail area you want to compute.
Decide if it's a left tail area or a right tail area.
If it's a left tail area, use
pnorm(z)in R to compute the value.
Standard Normal Tail Areas
We spell out the steps for computing tail areas under the standard normal density function.
First, draw a picture of the tail area you want to compute.
Decide if it's a left tail area or a right tail area.
If it's a left tail area, use
pnorm(z)in R to compute the value.If it's a right tail area, use
1 - pnorm(z)in R to compute the value.
Standard Normal Tail Areas
We spell out the steps for computing tail areas under the standard normal density function.
First, draw a picture of the tail area you want to compute.
Decide if it's a left tail area or a right tail area.
If it's a left tail area, use
pnorm(z)in R to compute the value.If it's a right tail area, use
1 - pnorm(z)in R to compute the value.
The next slide explains why this approach works.
The Meaning of pnorm
- The R command
pnorm(z)computes the area under the standard normal density function for values less than or equal to z. That is, it computes the tail area to the left of the valuez.
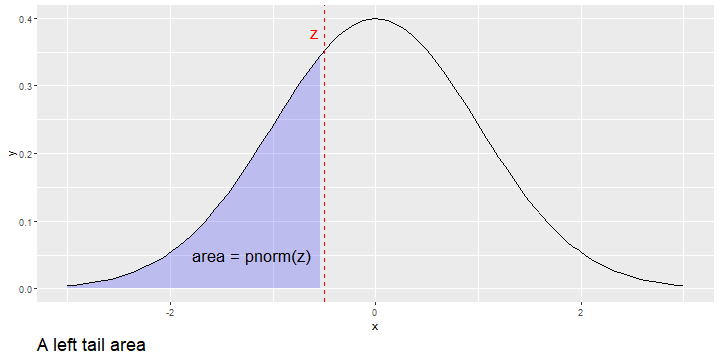
Right Tail Areas
- This figure explains why we use
1-pnorm(z)to compute right tail areas.
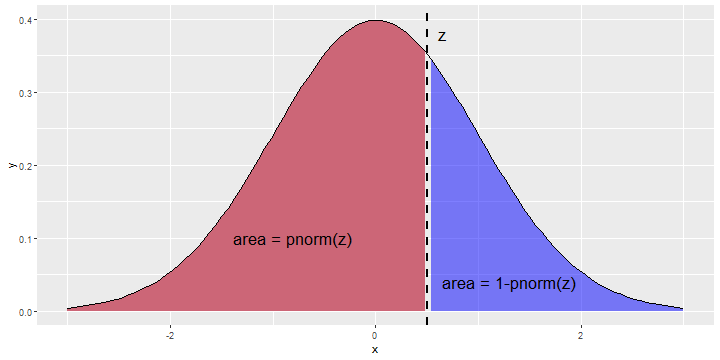
Right Tail Areas
- This figure explains why we use
1-pnorm(z)to compute right tail areas.

- Since the total area is 1 and
pnorm(z)gives the left tail area it must be that1-pnorm(z)gives the right tail area.
Left Tail Example
- What is the area under the standard normal density curve to the left of -2? That is, what is the area shown in the figure?
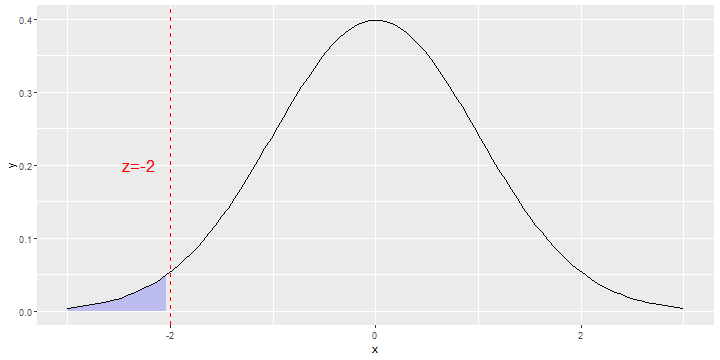
Left Tail Example
- What is the area under the standard normal density curve to the left of -2? That is, what is the area shown in the figure?

- It is
pnorm(-2) =0.0227501.
Right Tail Example
- What is the area under the standard normal density curve to the right of 1? That is, what is the area shown in the figure?
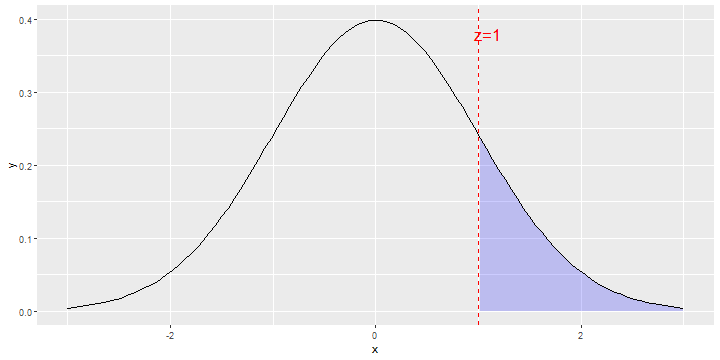
Right Tail Example
- What is the area under the standard normal density curve to the right of 1? That is, what is the area shown in the figure?

- It is
1-pnorm(1) =0.1586553.
Middle Areas
- You are probably curious as to how we can compute a "middle" area such as the one shown below.
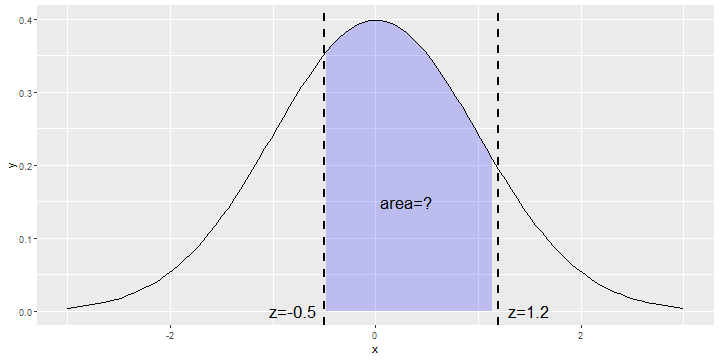
Middle Areas
- You are probably curious as to how we can compute a "middle" area such as the one shown below.

- The answer is simple, find the left and right tail areas and then subtract from 1.
Middle Area Example
- To compute the area shown:
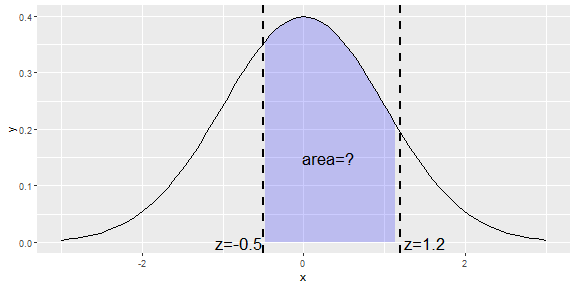
Middle Area Example
- To compute the area shown:

l_area <- pnorm(-0.5) # compute left tail arear_area <- 1 - pnorm(1.2) # copute right tail area(mid_area <- 1 - (l_area + r_area)) # subtract tails areas from 1## [1] 0.5763928Alternative Method for Mid Areas
- Notice that the following computation also finds the mid area shown on the previous slide
pnorm(1.2) - pnorm(-0.5)## [1] 0.5763928Alternative Method for Mid Areas
- Notice that the following computation also finds the mid area shown on the previous slide
pnorm(1.2) - pnorm(-0.5)## [1] 0.5763928- Take a minute to think about why this works and then we will discuss together.
Alternative Method for Mid Areas
- Notice that the following computation also finds the mid area shown on the previous slide
pnorm(1.2) - pnorm(-0.5)## [1] 0.5763928Take a minute to think about why this works and then we will discuss together.
What does
pnorm(1.2)represent? Draw the area under the standard normal density curve that it represents.
Alternative Method for Mid Areas
- Notice that the following computation also finds the mid area shown on the previous slide
pnorm(1.2) - pnorm(-0.5)## [1] 0.5763928Take a minute to think about why this works and then we will discuss together.
What does
pnorm(1.2)represent? Draw the area under the standard normal density curve that it represents.What does
pnorm(-0.5)represent? Draw the area under the standard normal density curve that it represents.
Alternative Method for Mid Areas
- Notice that the following computation also finds the mid area shown on the previous slide
pnorm(1.2) - pnorm(-0.5)## [1] 0.5763928Take a minute to think about why this works and then we will discuss together.
What does
pnorm(1.2)represent? Draw the area under the standard normal density curve that it represents.What does
pnorm(-0.5)represent? Draw the area under the standard normal density curve that it represents.Now what does the difference
pnorm(1.2) - pnorm(-0.5)represent?
Areas for General Normal Density Curves
- Suppose that X∼N(μ=10,σ=2.5). How can we find the left tail area the density curve corresponding to N(μ=10,σ=2.5) that lies to the left of x=7.3? This area is shown below.
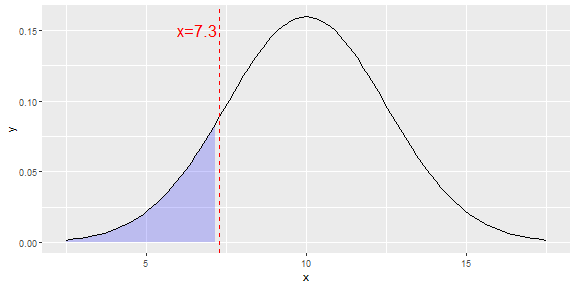
Areas for General Normal Density Curves
- Suppose that X∼N(μ=10,σ=2.5). How can we find the left tail area the density curve corresponding to N(μ=10,σ=2.5) that lies to the left of x=7.3? This area is shown below.

- The answer is, we first standardize to find z=x−μσ=7.3−102.5= -1.08, then we compute
pnorm(z) =0.1400711.
General Steps for Normal Curve Areas
- To compute the area under a normal density curve for N(μ,σ),
General Steps for Normal Curve Areas
To compute the area under a normal density curve for N(μ,σ),
- First draw a picture and determine if it is a left tail area, right tail area, or middle area.
General Steps for Normal Curve Areas
To compute the area under a normal density curve for N(μ,σ),
First draw a picture and determine if it is a left tail area, right tail area, or middle area.
Then standardize by subtracting the mean μ and dividing by the standard deviation σ.
General Steps for Normal Curve Areas
To compute the area under a normal density curve for N(μ,σ),
First draw a picture and determine if it is a left tail area, right tail area, or middle area.
Then standardize by subtracting the mean μ and dividing by the standard deviation σ.
Finally, use
pnormin R as we have explained over the last several slides.
General Steps for Normal Curve Areas
To compute the area under a normal density curve for N(μ,σ),
First draw a picture and determine if it is a left tail area, right tail area, or middle area.
Then standardize by subtracting the mean μ and dividing by the standard deviation σ.
Finally, use
pnormin R as we have explained over the last several slides.
We take a break from the slides to work out some examples together.
The 68-95-99.7 Rule
- The following figure shows the percentage of area under a normal curve that lies within 1, 2, and 3 standard deviations of the mean, respectively.

Worked Examples
- Let's take a break from lecture slides to go through some worked examples using the normal distribution.
Foundations for Inference
- We have now developed the probability tools we need to begin to discuss statistical inference. Before the next lecture, please watch this video: