Lecture 10
JMG
MATH 204
Linear Regression: Introduction
- Linear regression is a statistical method for fitting a line to data.
Linear Regression: Introduction
Linear regression is a statistical method for fitting a line to data.
Recall that a (non-vertical) line in the x,y-plane is determined by
y=slope×x+intercept
Linear Regression: Introduction
Linear regression is a statistical method for fitting a line to data.
Recall that a (non-vertical) line in the x,y-plane is determined by
y=slope×x+intercept
- There are two aspects to fitting a line to data that we will study:
Linear Regression: Introduction
Linear regression is a statistical method for fitting a line to data.
Recall that a (non-vertical) line in the x,y-plane is determined by
y=slope×x+intercept
There are two aspects to fitting a line to data that we will study:
- Estimating the slope and intercept values, and
Linear Regression: Introduction
Linear regression is a statistical method for fitting a line to data.
Recall that a (non-vertical) line in the x,y-plane is determined by
y=slope×x+intercept
There are two aspects to fitting a line to data that we will study:
Estimating the slope and intercept values, and
Assessing the uncertainty of our estimates for the slope and intercept values.
Linear Regression: Introduction
Linear regression is a statistical method for fitting a line to data.
Recall that a (non-vertical) line in the x,y-plane is determined by
y=slope×x+intercept
There are two aspects to fitting a line to data that we will study:
Estimating the slope and intercept values, and
Assessing the uncertainty of our estimates for the slope and intercept values.
In this lecture, we cover all of the concepts necessary to understand how to carry out and interpret linear regression.
Linear Regression: Introduction
Linear regression is a statistical method for fitting a line to data.
Recall that a (non-vertical) line in the x,y-plane is determined by
y=slope×x+intercept
There are two aspects to fitting a line to data that we will study:
Estimating the slope and intercept values, and
Assessing the uncertainty of our estimates for the slope and intercept values.
In this lecture, we cover all of the concepts necessary to understand how to carry out and interpret linear regression.
We encourage you to watch the video on the next slide to help in getting introduced to linear regression.
Regression Intro Video
Learning Objectives
- After this lecture, you should
Learning Objectives
After this lecture, you should
- Understand the basic principles of simple linear regression: parameter estimates, residuals, and correlation. (8.1, 8.2)
Learning Objectives
After this lecture, you should
Understand the basic principles of simple linear regression: parameter estimates, residuals, and correlation. (8.1, 8.2)
Know the conditions for least squares regression: linearity, normality, constant variance, and independence. (8.2)
Learning Objectives
After this lecture, you should
Understand the basic principles of simple linear regression: parameter estimates, residuals, and correlation. (8.1, 8.2)
Know the conditions for least squares regression: linearity, normality, constant variance, and independence. (8.2)
Know how to diagnose problems with a linear fit by least squares regression. (8.3)
Learning Objectives
After this lecture, you should
Understand the basic principles of simple linear regression: parameter estimates, residuals, and correlation. (8.1, 8.2)
Know the conditions for least squares regression: linearity, normality, constant variance, and independence. (8.2)
Know how to diagnose problems with a linear fit by least squares regression. (8.3)
Understand the methods of inference of least squares regression. (8.4)
Learning Objectives
After this lecture, you should
Understand the basic principles of simple linear regression: parameter estimates, residuals, and correlation. (8.1, 8.2)
Know the conditions for least squares regression: linearity, normality, constant variance, and independence. (8.2)
Know how to diagnose problems with a linear fit by least squares regression. (8.3)
Understand the methods of inference of least squares regression. (8.4)
Know how to obtain a linear fit using R with the
lmfunction.
Learning Objectives
After this lecture, you should
Understand the basic principles of simple linear regression: parameter estimates, residuals, and correlation. (8.1, 8.2)
Know the conditions for least squares regression: linearity, normality, constant variance, and independence. (8.2)
Know how to diagnose problems with a linear fit by least squares regression. (8.3)
Understand the methods of inference of least squares regression. (8.4)
Know how to obtain a linear fit using R with the
lmfunction.Be able to assess and interpret the results of a linear fit using R with the
lmfunction.
Simple Regression Model
- Simple linear regression models the relationship between two (numerical) variables x and y by the formula
y=β0+β1x+ϵ where
Simple Regression Model
- Simple linear regression models the relationship between two (numerical) variables x and y by the formula
y=β0+β1x+ϵ where
- β0 (intercept) and β1 (slope) are the model parameters
Simple Regression Model
- Simple linear regression models the relationship between two (numerical) variables x and y by the formula
y=β0+β1x+ϵ where
β0 (intercept) and β1 (slope) are the model parameters
ϵ is the error
Simple Regression Model
- Simple linear regression models the relationship between two (numerical) variables x and y by the formula
y=β0+β1x+ϵ where
β0 (intercept) and β1 (slope) are the model parameters
ϵ is the error
- The parameters are estimated using data and their point estimates are denoted by b0 (intercept estimate) and b1 (slope estimate).
Simple Regression Model
- Simple linear regression models the relationship between two (numerical) variables x and y by the formula
y=β0+β1x+ϵ where
β0 (intercept) and β1 (slope) are the model parameters
ϵ is the error
The parameters are estimated using data and their point estimates are denoted by b0 (intercept estimate) and b1 (slope estimate).
In linear regression, x is called the explanatory or predictor variable while y is called the response variable.
Simple Regression Model
- Simple linear regression models the relationship between two (numerical) variables x and y by the formula
y=β0+β1x+ϵ where
β0 (intercept) and β1 (slope) are the model parameters
ϵ is the error
The parameters are estimated using data and their point estimates are denoted by b0 (intercept estimate) and b1 (slope estimate).
In linear regression, x is called the explanatory or predictor variable while y is called the response variable.
Let's look at an example data set for which linear regression is a potentially useful model.
Australian Brushtail Possum

Australian Brushtail Possum

- The
possumdata set records measurements of 104 brushtail possums from Australia and New Guinea, the first few rows of the data are shown below
head(possum,4)## # A tibble: 4 x 8## site pop sex age head_l skull_w total_l tail_l## <int> <fct> <fct> <int> <dbl> <dbl> <dbl> <dbl>## 1 1 Vic m 8 94.1 60.4 89 36 ## 2 1 Vic f 6 92.5 57.6 91.5 36.5## 3 1 Vic f 6 94 60 95.5 39 ## 4 1 Vic f 6 93.2 57.1 92 38Possum Data Example
- Suppose that we as researchers are interested to study the relationship between the head length (
head_l) and total length (total_l) measurements of the brushtail possum of Australia.
Possum Data Example
Suppose that we as researchers are interested to study the relationship between the head length (
head_l) and total length (total_l) measurements of the brushtail possum of Australia.Note that head length (
head_l) and total length (total_l) are both (continuous) numerical variables.
Possum Data Example
Suppose that we as researchers are interested to study the relationship between the head length (
head_l) and total length (total_l) measurements of the brushtail possum of Australia.Note that head length (
head_l) and total length (total_l) are both (continuous) numerical variables.The next slide displays a scatterplot for
head_lversustotal_l.
Possum Data Scatterplot
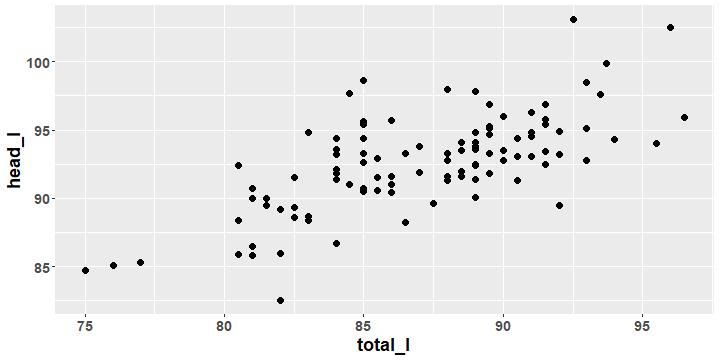
Possum Data Scatterplot

- Describe the features of any association that there appears to be between the two variables in the plot.
Possum Data Regression Line
- We have added the "best fit" line to the scatter plot of
head_lversustotal_l. Later we discuss how this line is obtained.
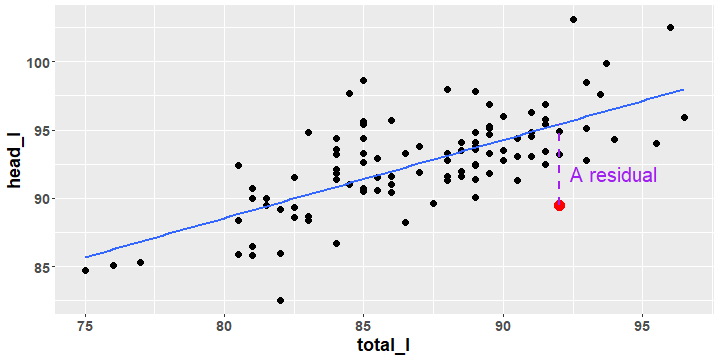
Possum Data Regression Line
- We have added the "best fit" line to the scatter plot of
head_lversustotal_l. Later we discuss how this line is obtained.

- A residual is the vertical distance between a data point and the best fit line. The next slide shows all of the residuals for the data.
Possum Regression Residuals
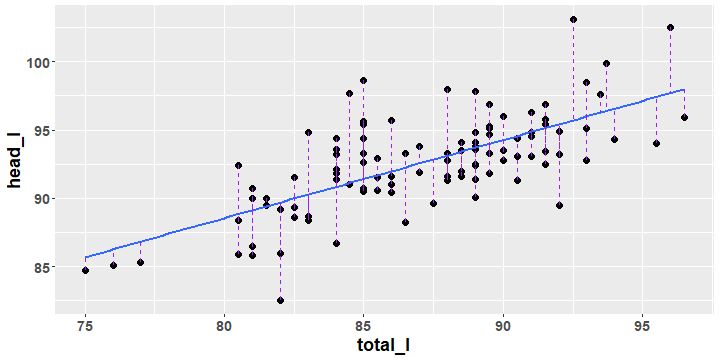
Possum Regression Residuals

- The best fit or regression line is the line that minimizes all of the residuals simultaneously.
Possum Regression Residual Plot
- A residual plot displays the residual values versus the x values from the data.
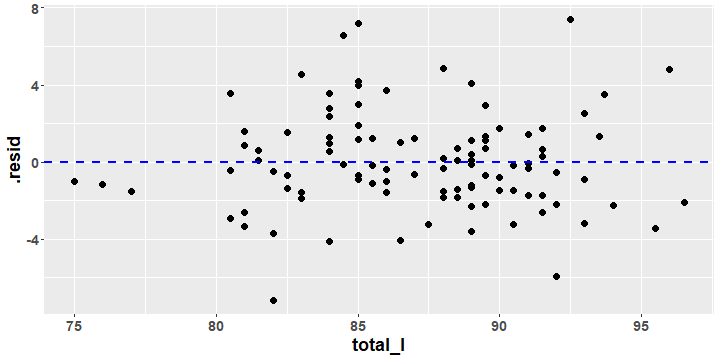
Possum Regression Residual Plot
- A residual plot displays the residual values versus the x values from the data.

- As we will see, residual plots play an important role in assessing the results of a regression model.
Fits and Residual Plots
- Let's look some linear fits and their corresponding residual plots.
Fits and Residual Plots
- Let's look some linear fits and their corresponding residual plots.

Fits and Residual Plots
- Let's look some linear fits and their corresponding residual plots.

- In the first column, the residuals show no obvious pattern, this is desirable. In the second column, the residuals show a pattern that suggests a linear model is inappropriate. In the third column, it's not clear if the linear fit is statistically significant.
Correlation
- Correlation, which always takes values between -1 and 1 is a statistic that describes the strength of the linear relationship between two variables. Correlation is denoted by R.
Correlation
Correlation, which always takes values between -1 and 1 is a statistic that describes the strength of the linear relationship between two variables. Correlation is denoted by R.
In R, correlation is computed with the
corcommand. For example, the correlation between thehead_landtotal_lvariables in thepossumdata set is computed as
cor(possum$head_l,possum$total_l)## [1] 0.6910937Correlation
Correlation, which always takes values between -1 and 1 is a statistic that describes the strength of the linear relationship between two variables. Correlation is denoted by R.
In R, correlation is computed with the
corcommand. For example, the correlation between thehead_landtotal_lvariables in thepossumdata set is computed as
cor(possum$head_l,possum$total_l)## [1] 0.6910937- The plot in the next slide shows several scatter plots together with the corresponding correlation value.
Correlation Illustrations

Strongly Related Variables with Weak Correlations
- It is important to note that two variables may have a strong association even if their correlation is relatively weak. This is because correlation measures linear association and variables may be a strong nonlinear association.
Strongly Related Variables with Weak Correlations
- It is important to note that two variables may have a strong association even if their correlation is relatively weak. This is because correlation measures linear association and variables may be a strong nonlinear association.

Least Squares Regression
- We now begin to discuss the details of how to fit a simple linear regression model to data.
Least Squares Regression
We now begin to discuss the details of how to fit a simple linear regression model to data.
The approach we take is called least squares regression.
Least Squares Regression
We now begin to discuss the details of how to fit a simple linear regression model to data.
The approach we take is called least squares regression.
The idea is to chose parameter estimates that minimize all of the residuals simultaneously. That is, for each observed data point (xi,yi), we find b0 and b1 such that if ^yi=b0+b1xi, then
RSS=n∑i=1(^yi−yi)2
is as small as possible.
Least Squares Regression
We now begin to discuss the details of how to fit a simple linear regression model to data.
The approach we take is called least squares regression.
The idea is to chose parameter estimates that minimize all of the residuals simultaneously. That is, for each observed data point (xi,yi), we find b0 and b1 such that if ^yi=b0+b1xi, then
RSS=n∑i=1(^yi−yi)2
is as small as possible.
- For this to work out well, several conditions need to be met. These conditions are spelled out on the next slide.
Conditions for Least Squares
- Linearity. The data should show a linear trend.
Conditions for Least Squares
Linearity. The data should show a linear trend.
Normality. Generally, the distribution of the residuals should be close to normal.
Conditions for Least Squares
Linearity. The data should show a linear trend.
Normality. Generally, the distribution of the residuals should be close to normal.
Constant Variance. The variability of points around the least squares line remains roughly constant. Residual plots are a good way to check this condition.
Conditions for Least Squares
Linearity. The data should show a linear trend.
Normality. Generally, the distribution of the residuals should be close to normal.
Constant Variance. The variability of points around the least squares line remains roughly constant. Residual plots are a good way to check this condition.
Independence. We want to avoid fitting a line to data via least squares whenever there is dependence between consecutive data points.
Conditions for Least Squares
Linearity. The data should show a linear trend.
Normality. Generally, the distribution of the residuals should be close to normal.
Constant Variance. The variability of points around the least squares line remains roughly constant. Residual plots are a good way to check this condition.
Independence. We want to avoid fitting a line to data via least squares whenever there is dependence between consecutive data points.
The next slide shows plot of data where at least one of the conditions for least squares regression fails to hold.
Regression Assumption Failures

Regression Assumption Failures

- In the first column, the linearity condition fails. In the second column, the normality condition fails.
Regression Assumption Failures

In the first column, the linearity condition fails. In the second column, the normality condition fails.
In the third column, the constant variance condition fails. In the fourth column, the independence condition fails.
Regression Assumption Failures

In the first column, the linearity condition fails. In the second column, the normality condition fails.
In the third column, the constant variance condition fails. In the fourth column, the independence condition fails.
Notice how in each case, the residual plot can be used to diagnose problems with a least squares linear regression fit.
Fitting a Linear Model
- For simple least squares linear regression with one predictor variable ( x ), one can fit the model to data "by hand". The mathematical formula is
b1=sysxR,
b0=¯y−b1¯x,
where
- R is the correlation between x and y,
Fitting a Linear Model
- For simple least squares linear regression with one predictor variable ( x ), one can fit the model to data "by hand". The mathematical formula is
b1=sysxR,
b0=¯y−b1¯x,
where
R is the correlation between x and y,
sy and sx are the sample standard deviations for y and x, and
Fitting a Linear Model
- For simple least squares linear regression with one predictor variable ( x ), one can fit the model to data "by hand". The mathematical formula is
b1=sysxR,
b0=¯y−b1¯x,
where
R is the correlation between x and y,
sy and sx are the sample standard deviations for y and x, and
¯y and ¯x are the sample means for y and x.
Fitting a Linear Model
- For simple least squares linear regression with one predictor variable ( x ), one can fit the model to data "by hand". The mathematical formula is
b1=sysxR,
b0=¯y−b1¯x,
where
R is the correlation between x and y,
sy and sx are the sample standard deviations for y and x, and
¯y and ¯x are the sample means for y and x.
- Let's apply these formulas to the
possumdata set with x thetotal_lvariable and y thehead_lvariable.
Applying the Regression Formulas
- We need to compute the correlation, sample means, and sample standard deviations:
x <- possum$total_l; y <- possum$head_lx_bar <- mean(x); y_bar <- mean(y)s_x <- sd(x); s_y <- sd(y)R <- cor(x,y)Applying the Regression Formulas
- We need to compute the correlation, sample means, and sample standard deviations:
x <- possum$total_l; y <- possum$head_lx_bar <- mean(x); y_bar <- mean(y)s_x <- sd(x); s_y <- sd(y)R <- cor(x,y)- Now we can compute our estimates b0 and b1:
(b_1 <- (s_y/s_x)*R)## [1] 0.5729013(b_0 <- y_bar - b_1*x_bar)## [1] 42.70979Applying the Regression Formulas
- We need to compute the correlation, sample means, and sample standard deviations:
x <- possum$total_l; y <- possum$head_lx_bar <- mean(x); y_bar <- mean(y)s_x <- sd(x); s_y <- sd(y)R <- cor(x,y)- Now we can compute our estimates b0 and b1:
(b_1 <- (s_y/s_x)*R)## [1] 0.5729013(b_0 <- y_bar - b_1*x_bar)## [1] 42.70979- There is an R command,
lm(linear model) that will compute these values and much more for us.
The lm Command
- Let's see an example of how the
lmcommand is used:
lm(head_l ~ total_l, data=possum)## ## Call:## lm(formula = head_l ~ total_l, data = possum)## ## Coefficients:## (Intercept) total_l ## 42.7098 0.5729The lm Command
- Let's see an example of how the
lmcommand is used:
lm(head_l ~ total_l, data=possum)## ## Call:## lm(formula = head_l ~ total_l, data = possum)## ## Coefficients:## (Intercept) total_l ## 42.7098 0.5729- Notice that this returns the point estimate values for b0 (Intercept) and the slope b1, and that these values are the same as what we obtained using the mathematical formulas on the last slide.
Interpreting Model Parameters
- For a linear model,
Interpreting Model Parameters
For a linear model,
- The slope describes the estimate difference in the y variable if the explanatory variable x for a case happened to be one unit larger.
Interpreting Model Parameters
For a linear model,
The slope describes the estimate difference in the y variable if the explanatory variable x for a case happened to be one unit larger.
The intercept describes the average outcome of y if x=0 and the linear model is valid all the way to x=0, which in many applications is not the case.
Interpreting Model Parameters
For a linear model,
The slope describes the estimate difference in the y variable if the explanatory variable x for a case happened to be one unit larger.
The intercept describes the average outcome of y if x=0 and the linear model is valid all the way to x=0, which in many applications is not the case.
To evaluate the strength of a linear fit, we compute R2 (R-squared). The value of R2 tells us the percent of variation in the response that is explained by the explanatory variable.
Interpreting Model Parameters
For a linear model,
The slope describes the estimate difference in the y variable if the explanatory variable x for a case happened to be one unit larger.
The intercept describes the average outcome of y if x=0 and the linear model is valid all the way to x=0, which in many applications is not the case.
To evaluate the strength of a linear fit, we compute R2 (R-squared). The value of R2 tells us the percent of variation in the response that is explained by the explanatory variable.
There are some pitfalls in interpreting the results of a linear model. In particular,
Interpreting Model Parameters
For a linear model,
The slope describes the estimate difference in the y variable if the explanatory variable x for a case happened to be one unit larger.
The intercept describes the average outcome of y if x=0 and the linear model is valid all the way to x=0, which in many applications is not the case.
To evaluate the strength of a linear fit, we compute R2 (R-squared). The value of R2 tells us the percent of variation in the response that is explained by the explanatory variable.
There are some pitfalls in interpreting the results of a linear model. In particular,
- Applying a model to estimate values outside of the realm of the original data is called extrapolation. Generally, extrapolation is unreliable.
Interpreting Model Parameters
For a linear model,
The slope describes the estimate difference in the y variable if the explanatory variable x for a case happened to be one unit larger.
The intercept describes the average outcome of y if x=0 and the linear model is valid all the way to x=0, which in many applications is not the case.
To evaluate the strength of a linear fit, we compute R2 (R-squared). The value of R2 tells us the percent of variation in the response that is explained by the explanatory variable.
There are some pitfalls in interpreting the results of a linear model. In particular,
Applying a model to estimate values outside of the realm of the original data is called extrapolation. Generally, extrapolation is unreliable.
In many cases, even when there is a real association between variables, we cannot interpret a causal connection between the variables.
Example
- Before we discuss further details of regression, let's look at a detailed example of fitting and interpreting a linear model.
Example
Before we discuss further details of regression, let's look at a detailed example of fitting and interpreting a linear model.
We will look at a linear model for the data set,
cheddarfrom thefarawaypackage.
Example
Before we discuss further details of regression, let's look at a detailed example of fitting and interpreting a linear model.
We will look at a linear model for the data set,
cheddarfrom thefarawaypackage.Let's do this example together in RStudio.
Outlier Issues
- Outliers in regression are observations that fall far from the cloud of points.
Outlier Issues
- Outliers in regression are observations that fall far from the cloud of points.
- Outliers can have a strong influence on the least squares line.
Outlier Issues
- Outliers in regression are observations that fall far from the cloud of points.
Outliers can have a strong influence on the least squares line.
Points that fall horizontally away from the center of the cloud tend to pull harder on the line, so we call them points with high leverage.
Outlier Issues
- Outliers in regression are observations that fall far from the cloud of points.
Outliers can have a strong influence on the least squares line.
Points that fall horizontally away from the center of the cloud tend to pull harder on the line, so we call them points with high leverage.
A data point is called an influential point if, had we fitted the line without it, the influential point would have been unusually far from the least squares line.
Outlier Issues
- Outliers in regression are observations that fall far from the cloud of points.
Outliers can have a strong influence on the least squares line.
Points that fall horizontally away from the center of the cloud tend to pull harder on the line, so we call them points with high leverage.
A data point is called an influential point if, had we fitted the line without it, the influential point would have been unusually far from the least squares line.
The next slide shows data with outliers together with the corresponding regression line and residual plot.
Regression Outliers

Inference for Regression
- Recall that a simple linear model has the form
y=β0+β1x+ϵ
Inference for Regression
- Recall that a simple linear model has the form
y=β0+β1x+ϵ
- Least squares is a method for obtaining point estimates b0 and b1 for the parameters β0 and β1. Thus, β0 and β1 are unknowns that correspond to population values that we want to infer information about.
Inference for Regression
- Recall that a simple linear model has the form
y=β0+β1x+ϵ
Least squares is a method for obtaining point estimates b0 and b1 for the parameters β0 and β1. Thus, β0 and β1 are unknowns that correspond to population values that we want to infer information about.
A somewhat subtle point is that we also do not know the population standard deviation σ for the error ϵ. This is an additional model parameter.
Inference for Regression
- Recall that a simple linear model has the form
y=β0+β1x+ϵ
Least squares is a method for obtaining point estimates b0 and b1 for the parameters β0 and β1. Thus, β0 and β1 are unknowns that correspond to population values that we want to infer information about.
A somewhat subtle point is that we also do not know the population standard deviation σ for the error ϵ. This is an additional model parameter.
We would like answers to the following questions:
Inference for Regression
- Recall that a simple linear model has the form
y=β0+β1x+ϵ
Least squares is a method for obtaining point estimates b0 and b1 for the parameters β0 and β1. Thus, β0 and β1 are unknowns that correspond to population values that we want to infer information about.
A somewhat subtle point is that we also do not know the population standard deviation σ for the error ϵ. This is an additional model parameter.
We would like answers to the following questions:
- How do we obtain confidence intervals for β0 and β1, specifically how to we get the standard error?
Inference for Regression
- Recall that a simple linear model has the form
y=β0+β1x+ϵ
Least squares is a method for obtaining point estimates b0 and b1 for the parameters β0 and β1. Thus, β0 and β1 are unknowns that correspond to population values that we want to infer information about.
A somewhat subtle point is that we also do not know the population standard deviation σ for the error ϵ. This is an additional model parameter.
We would like answers to the following questions:
How do we obtain confidence intervals for β0 and β1, specifically how to we get the standard error?
How do we conduct hypothesis tests related to the parameters β0 and β1?
Confidence Intervals for Model Coefficients
- Fact: The sampling distribution for estimates for β0 and β1 is a t-distribution. So we can obtain confidence intervals with
bi±t∗df×SEbi
Confidence Intervals for Model Coefficients
- Fact: The sampling distribution for estimates for β0 and β1 is a t-distribution. So we can obtain confidence intervals with
bi±t∗df×SEbi
- All the numerical information you need to obtain confidence intervals for β0 and β1 is provided in the output of the
summarycommand for a linear model fit withlm.
Confidence Intervals for Model Coefficients
- Fact: The sampling distribution for estimates for β0 and β1 is a t-distribution. So we can obtain confidence intervals with
bi±t∗df×SEbi
All the numerical information you need to obtain confidence intervals for β0 and β1 is provided in the output of the
summarycommand for a linear model fit withlm.Suppose we fit a linear model for the
possumdata again:
(lm_fit <- lm(head_l ~ total_l, data=possum))## ## Call:## lm(formula = head_l ~ total_l, data = possum)## ## Coefficients:## (Intercept) total_l ## 42.7098 0.5729Confidence Intervals for Model Coefficients
- Fact: The sampling distribution for estimates for β0 and β1 is a t-distribution. So we can obtain confidence intervals with
bi±t∗df×SEbi
All the numerical information you need to obtain confidence intervals for β0 and β1 is provided in the output of the
summarycommand for a linear model fit withlm.Suppose we fit a linear model for the
possumdata again:
(lm_fit <- lm(head_l ~ total_l, data=possum))## ## Call:## lm(formula = head_l ~ total_l, data = possum)## ## Coefficients:## (Intercept) total_l ## 42.7098 0.5729- On the next slide, we print the output of
summary(lm_fit)
lm summary output
summary(lm_fit)## ## Call:## lm(formula = head_l ~ total_l, data = possum)## ## Residuals:## Min 1Q Median 3Q Max ## -7.1877 -1.5340 -0.3345 1.2788 7.3968 ## ## Coefficients:## Estimate Std. Error t value Pr(>|t|) ## (Intercept) 42.70979 5.17281 8.257 5.66e-13 ***## total_l 0.57290 0.05933 9.657 4.68e-16 ***## ---## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1## ## Residual standard error: 2.595 on 102 degrees of freedom## Multiple R-squared: 0.4776, Adjusted R-squared: 0.4725 ## F-statistic: 93.26 on 1 and 102 DF, p-value: 4.681e-16lm summary output
summary(lm_fit)## ## Call:## lm(formula = head_l ~ total_l, data = possum)## ## Residuals:## Min 1Q Median 3Q Max ## -7.1877 -1.5340 -0.3345 1.2788 7.3968 ## ## Coefficients:## Estimate Std. Error t value Pr(>|t|) ## (Intercept) 42.70979 5.17281 8.257 5.66e-13 ***## total_l 0.57290 0.05933 9.657 4.68e-16 ***## ---## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1## ## Residual standard error: 2.595 on 102 degrees of freedom## Multiple R-squared: 0.4776, Adjusted R-squared: 0.4725 ## F-statistic: 93.26 on 1 and 102 DF, p-value: 4.681e-16- For obtaining a confidence interval, the relevant information is provided by
Estimate,Std. Error, and the reported degrees of freedom.
Regression CI Example
- Based on the information provided in the
summarycommand output, we can construct confidence intervals for β0 and β1. First we observe that the degrees of freedom is 102, then the t∗102 value for a 95% CI is
(t_ast <- -qt((1.0-0.95)/2,df=102))## [1] 1.983495Regression CI Example
- Based on the information provided in the
summarycommand output, we can construct confidence intervals for β0 and β1. First we observe that the degrees of freedom is 102, then the t∗102 value for a 95% CI is
(t_ast <- -qt((1.0-0.95)/2,df=102))## [1] 1.983495- Now we can obtain our confidence intervals for β0 and β1:
(beta_0_CI <- 42.71 + 1.98*c(-1,1)*5.17)## [1] 32.4734 52.9466(beta_1_CI <- 0.57 + 1.98*c(-1,1)*0.06)## [1] 0.4512 0.6888Hypothesis Testing for Linear Regression
- There are actually several types of hypothesis tests one can conduct relating to linear regression models.
Hypothesis Testing for Linear Regression
There are actually several types of hypothesis tests one can conduct relating to linear regression models.
The most common test is of the form
- H0:β1=0. The true linear model has slope zero. Versus
Hypothesis Testing for Linear Regression
There are actually several types of hypothesis tests one can conduct relating to linear regression models.
The most common test is of the form
H0:β1=0. The true linear model has slope zero. Versus
HA:β1≠0. The true linear model has a slope different than zero.
Hypothesis Testing for Linear Regression
There are actually several types of hypothesis tests one can conduct relating to linear regression models.
The most common test is of the form
H0:β1=0. The true linear model has slope zero. Versus
HA:β1≠0. The true linear model has a slope different than zero.
The
summarycommand output includes a p-value for testing such a hypothesis. However, be aware that thelmcommand does not check whether the conditions for a linear model are met and the results for inference on model parameters is only valid if the conditions for a linear model are met.
Hypothesis Test for possum Data
- Again, the output for
summary(lm_fit)is
summary(lm_fit)## ## Call:## lm(formula = head_l ~ total_l, data = possum)## ## Residuals:## Min 1Q Median 3Q Max ## -7.1877 -1.5340 -0.3345 1.2788 7.3968 ## ## Coefficients:## Estimate Std. Error t value Pr(>|t|) ## (Intercept) 42.70979 5.17281 8.257 5.66e-13 ***## total_l 0.57290 0.05933 9.657 4.68e-16 ***## ---## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1## ## Residual standard error: 2.595 on 102 degrees of freedom## Multiple R-squared: 0.4776, Adjusted R-squared: 0.4725 ## F-statistic: 93.26 on 1 and 102 DF, p-value: 4.681e-16Hypothesis Test for possum Data
- Again, the output for
summary(lm_fit)is
summary(lm_fit)## ## Call:## lm(formula = head_l ~ total_l, data = possum)## ## Residuals:## Min 1Q Median 3Q Max ## -7.1877 -1.5340 -0.3345 1.2788 7.3968 ## ## Coefficients:## Estimate Std. Error t value Pr(>|t|) ## (Intercept) 42.70979 5.17281 8.257 5.66e-13 ***## total_l 0.57290 0.05933 9.657 4.68e-16 ***## ---## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1## ## Residual standard error: 2.595 on 102 degrees of freedom## Multiple R-squared: 0.4776, Adjusted R-squared: 0.4725 ## F-statistic: 93.26 on 1 and 102 DF, p-value: 4.681e-16- The p-value corresponding to the slope estimate b1 is much smaller than 0.05 so we will decide to reject the null hypothesis H0:β1=0 at the α=0.05 significance level.
Inference for Regression Video
- Please watch this video to gain further perspective on inference for linear regression:
More R For Linear Models
- To fit a linear model in R we use the
lmcommand. The necessary input is a formula of the formy ~ xand the data. Thesummarycommand outputs all of the information relevant for inferential purposes.
More R For Linear Models
To fit a linear model in R we use the
lmcommand. The necessary input is a formula of the formy ~ xand the data. Thesummarycommand outputs all of the information relevant for inferential purposes.However, the output from
summaryis not necessarily formatted in the most convenient way.
More R For Linear Models
To fit a linear model in R we use the
lmcommand. The necessary input is a formula of the formy ~ xand the data. Thesummarycommand outputs all of the information relevant for inferential purposes.However, the output from
summaryis not necessarily formatted in the most convenient way.Another approach to working with regression model output is provided by functions in the
broompackage. For example, thetidyfunction frombroomdisplays the results of the model fit:
tidy(lm_fit)## # A tibble: 2 x 5## term estimate std.error statistic p.value## <chr> <dbl> <dbl> <dbl> <dbl>## 1 (Intercept) 42.7 5.17 8.26 5.66e-13## 2 total_l 0.573 0.0593 9.66 4.68e-16More R For Linear Models
To fit a linear model in R we use the
lmcommand. The necessary input is a formula of the formy ~ xand the data. Thesummarycommand outputs all of the information relevant for inferential purposes.However, the output from
summaryis not necessarily formatted in the most convenient way.Another approach to working with regression model output is provided by functions in the
broompackage. For example, thetidyfunction frombroomdisplays the results of the model fit:
tidy(lm_fit)## # A tibble: 2 x 5## term estimate std.error statistic p.value## <chr> <dbl> <dbl> <dbl> <dbl>## 1 (Intercept) 42.7 5.17 8.26 5.66e-13## 2 total_l 0.573 0.0593 9.66 4.68e-16- Let's go to R together, work some more examples, and learn to work with the
broomfunctions.
Worked Examples
- Let's work some more examples relating to linear regression.
Comparing Many Means
- In previous lectures, we studied inference for a difference of means. There are also statistical methods for comparing more than two means. The primary method is called analysis of variance (ANOVA), see 7.5.
Comparing Many Means
In previous lectures, we studied inference for a difference of means. There are also statistical methods for comparing more than two means. The primary method is called analysis of variance (ANOVA), see 7.5.
ANOVA uses a single hypothesis to check whether the means across many groups are equal:
Comparing Many Means
In previous lectures, we studied inference for a difference of means. There are also statistical methods for comparing more than two means. The primary method is called analysis of variance (ANOVA), see 7.5.
ANOVA uses a single hypothesis to check whether the means across many groups are equal:
H0:μ1=μ2=⋯=μk. The mean outcome is the same across all groups. Versus
HA: At least one mean is different.
Comparing Many Means
In previous lectures, we studied inference for a difference of means. There are also statistical methods for comparing more than two means. The primary method is called analysis of variance (ANOVA), see 7.5.
ANOVA uses a single hypothesis to check whether the means across many groups are equal:
H0:μ1=μ2=⋯=μk. The mean outcome is the same across all groups. Versus
HA: At least one mean is different.
We must check three conditions for ANOVA:
Comparing Many Means
In previous lectures, we studied inference for a difference of means. There are also statistical methods for comparing more than two means. The primary method is called analysis of variance (ANOVA), see 7.5.
ANOVA uses a single hypothesis to check whether the means across many groups are equal:
H0:μ1=μ2=⋯=μk. The mean outcome is the same across all groups. Versus
HA: At least one mean is different.
We must check three conditions for ANOVA:
(1) Observations are independent across groups. (2) The data within each group are nearly normal. (3) The variability across each group is about equal.
Example Data Motivating ANOVA
- Let's consider our chicken feed data again. The first few rows are shown below:
head(chickwts)## weight feed## 1 179 horsebean## 2 160 horsebean## 3 136 horsebean## 4 227 horsebean## 5 217 horsebean## 6 168 horsebeanExample Data Motivating ANOVA
- Let's consider our chicken feed data again. The first few rows are shown below:
head(chickwts)## weight feed## 1 179 horsebean## 2 160 horsebean## 3 136 horsebean## 4 227 horsebean## 5 217 horsebean## 6 168 horsebean- The next slide show a plot of this data.
Plot of Data
chickwts %>% ggplot(aes(x=feed,y=weight)) + geom_boxplot()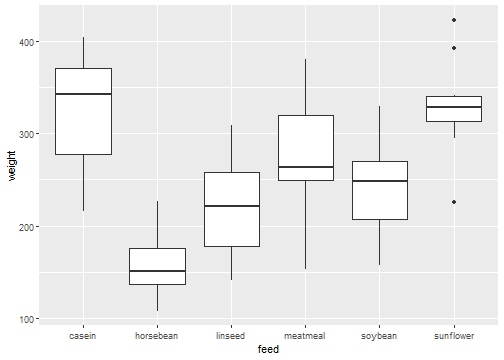
Plot of Data
chickwts %>% ggplot(aes(x=feed,y=weight)) + geom_boxplot()
- It appears that the mean weight is not the same for all groups of chickens. The question we would like to have an answer to is, is the observed difference significant?
The F Statistics and the F-Test
- Analysis of variance (ANOVA) is used to test whether the mean outcome differs across 2 or more groups.
The F Statistics and the F-Test
Analysis of variance (ANOVA) is used to test whether the mean outcome differs across 2 or more groups.
ANOVA uses a test statistic denoted by F, which represents a standardized ratio of variability in the sample means relative to the variability within groups.
The F Statistics and the F-Test
Analysis of variance (ANOVA) is used to test whether the mean outcome differs across 2 or more groups.
ANOVA uses a test statistic denoted by F, which represents a standardized ratio of variability in the sample means relative to the variability within groups.
ANOVA uses an F distribution to compute a p-value that corresponds to the probability of observing an F statistic value that is as or more extreme than the sample F statistic value under the assumption that the null hypothesis is true.
The F Statistics and the F-Test
Analysis of variance (ANOVA) is used to test whether the mean outcome differs across 2 or more groups.
ANOVA uses a test statistic denoted by F, which represents a standardized ratio of variability in the sample means relative to the variability within groups.
ANOVA uses an F distribution to compute a p-value that corresponds to the probability of observing an F statistic value that is as or more extreme than the sample F statistic value under the assumption that the null hypothesis is true.
We will see how to conduct ANOVA and an F-test using R.
The F Statistics and the F-Test
Analysis of variance (ANOVA) is used to test whether the mean outcome differs across 2 or more groups.
ANOVA uses a test statistic denoted by F, which represents a standardized ratio of variability in the sample means relative to the variability within groups.
ANOVA uses an F distribution to compute a p-value that corresponds to the probability of observing an F statistic value that is as or more extreme than the sample F statistic value under the assumption that the null hypothesis is true.
We will see how to conduct ANOVA and an F-test using R.
Before conducting ANOVA, we should discuss the necessary conditions for an ANOVA analysis.
Conditions for ANOVA
- There are three conditions we must check for an ANOVA:
Conditions for ANOVA
There are three conditions we must check for an ANOVA:
- Independence. If the data are a simple random sample, this condition is satisfied.
Conditions for ANOVA
There are three conditions we must check for an ANOVA:
Independence. If the data are a simple random sample, this condition is satisfied.
Normality. As with one- and two-sample testing for means, the normality assumption is especially important when the sample size is small. Grouped histograms are a good way to diagnose potential problems with the normality assumption for ANOVA.
Conditions for ANOVA
There are three conditions we must check for an ANOVA:
Independence. If the data are a simple random sample, this condition is satisfied.
Normality. As with one- and two-sample testing for means, the normality assumption is especially important when the sample size is small. Grouped histograms are a good way to diagnose potential problems with the normality assumption for ANOVA.
Constant variance. The variance in the groups should be close to equal. This assumption can be checked with side-by-side box plots.
ANOVA Examples
- Let's see some examples of conducting ANOVA. We will do this together in R.
Next Time: Inference for Categorical Data
- Now that we have explored a lot about inference for numerical data, our next topic is some methods of inference for categorical data. The included video is a good place to start: