+ - 0:00:00
Notes for current slide
Notes for next slide

Lecture 11

JMG

MATH 204

1 / 23

Inference for Categorical Data

In this lecture, we will examine two new inferential techniques:

2 / 23

Inference for Categorical Data

In this lecture, we will examine two new inferential techniques:

  • Testing for goodness of fit using chi-square, which is applied to a categorical variable with more than two levels. This is commonly used in two circumstances:
2 / 23

Inference for Categorical Data

In this lecture, we will examine two new inferential techniques:

  • Testing for goodness of fit using chi-square, which is applied to a categorical variable with more than two levels. This is commonly used in two circumstances:

    • Given a sample of cases that can be classified into several groups, determine if the sample is representative of the general population.
2 / 23

Inference for Categorical Data

In this lecture, we will examine two new inferential techniques:

  • Testing for goodness of fit using chi-square, which is applied to a categorical variable with more than two levels. This is commonly used in two circumstances:

    • Given a sample of cases that can be classified into several groups, determine if the sample is representative of the general population.

    • Evaluate whether data resemble a particular distribution, such as a normal distribution or a geometric distribution.

2 / 23

Inference for Categorical Data

In this lecture, we will examine two new inferential techniques:

  • Testing for goodness of fit using chi-square, which is applied to a categorical variable with more than two levels. This is commonly used in two circumstances:

    • Given a sample of cases that can be classified into several groups, determine if the sample is representative of the general population.

    • Evaluate whether data resemble a particular distribution, such as a normal distribution or a geometric distribution.

  • Testing for independence in two-way tables.

2 / 23

Learning Objectives

  • In this lecture, we cover some inferential techniques for categorical data. After this lecture you should be able to
3 / 23

Learning Objectives

  • In this lecture, we cover some inferential techniques for categorical data. After this lecture you should be able to

    • Identify one-way and two-way table problems.
3 / 23

Learning Objectives

  • In this lecture, we cover some inferential techniques for categorical data. After this lecture you should be able to

    • Identify one-way and two-way table problems.

    • Work with a chi-square statistic and distribution.

3 / 23

Learning Objectives

  • In this lecture, we cover some inferential techniques for categorical data. After this lecture you should be able to

    • Identify one-way and two-way table problems.

    • Work with a chi-square statistic and distribution.

    • Use the chisq.test function in R to conduct hypothesis tests.

3 / 23

Video on Goodness of Fit

4 / 23

Video on Two-Way Tables

5 / 23

Motivating Example

Consider the following data:

6 / 23

Motivating Example

Consider the following data:

race black hispanic white other total
Representation in juries 26.00 25.00 205.00 19.00 275
Registered voters 0.07 0.12 0.72 0.09 1
6 / 23

Motivating Example

Consider the following data:

race black hispanic white other total
Representation in juries 26.00 25.00 205.00 19.00 275
Registered voters 0.07 0.12 0.72 0.09 1

We can compute the proportions for the data:

## # A tibble: 4 x 3
##   race         n      p
##   <fct>    <int>  <dbl>
## 1 black       26 0.0945
## 2 hispanic    25 0.0909
## 3 other       19 0.0691
## 4 white      205 0.745
6 / 23

Motivating Example

Consider the following data:

race black hispanic white other total
Representation in juries 26.00 25.00 205.00 19.00 275
Registered voters 0.07 0.12 0.72 0.09 1

We can compute the proportions for the data:

## # A tibble: 4 x 3
##   race         n      p
##   <fct>    <int>  <dbl>
## 1 black       26 0.0945
## 2 hispanic    25 0.0909
## 3 other       19 0.0691
## 4 white      205 0.745
  • We would like to know if the jury is representative of the population.
6 / 23

Motivating Example

Consider the following data:

race black hispanic white other total
Representation in juries 26.00 25.00 205.00 19.00 275
Registered voters 0.07 0.12 0.72 0.09 1

We can compute the proportions for the data:

## # A tibble: 4 x 3
##   race         n      p
##   <fct>    <int>  <dbl>
## 1 black       26 0.0945
## 2 hispanic    25 0.0909
## 3 other       19 0.0691
## 4 white      205 0.745

  • We would like to know if the jury is representative of the population.

  • This problem illustrates "Given a sample of cases that can be classified into several groups, determine if the sample is representative of the general population."

6 / 23

One-Way Tables

  • If we were to take the bottom row of the table on the last slide as the assumed true proportions, then we would expect to get the following so-called one-way table:
race black hispanic white other total
Observed count 26.00 25 205 19.00 275
Expected count 19.25 33 198 24.75 275
7 / 23

One-Way Tables

  • If we were to take the bottom row of the table on the last slide as the assumed true proportions, then we would expect to get the following so-called one-way table:
race black hispanic white other total
Observed count 26.00 25 205 19.00 275
Expected count 19.25 33 198 24.75 275
  • From a one-way table we can produce a test statistic that follows a well-known distribution. Specifically, we compute

(26−19.25)219.25+(25−33)233+(205−198)2198+(19−24.75)224.75

7 / 23

One-Way Tables

  • If we were to take the bottom row of the table on the last slide as the assumed true proportions, then we would expect to get the following so-called one-way table:
race black hispanic white other total
Observed count 26.00 25 205 19.00 275
Expected count 19.25 33 198 24.75 275
  • From a one-way table we can produce a test statistic that follows a well-known distribution. Specifically, we compute

(26−19.25)219.25+(25−33)233+(205−198)2198+(19−24.75)224.75

  • This value is
(26-19.25)^2/19.25 + (25-33)^2/33 + (205-198)^2/198 + (19-24.75)^2/24.75
## [1] 5.88961
7 / 23

chi-Square Distributions

  • In order to conduct inferences on data corresponding to one-way tables, we need to use a new distribution function called a chi-square distribution. Such distributions are characterized by a parameter called degrees of freedom. Below we plot a chi-square density function with 3 degrees of freedom:
gf_dist("chisq",df=3)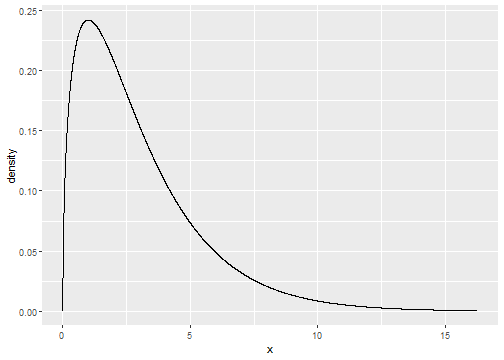

8 / 23

chi-Square for Different df's

9 / 23

chi-Square Test Conditions

  • In order to use a chi-square distribution to compute a p-value, we need to check two conditions:
10 / 23

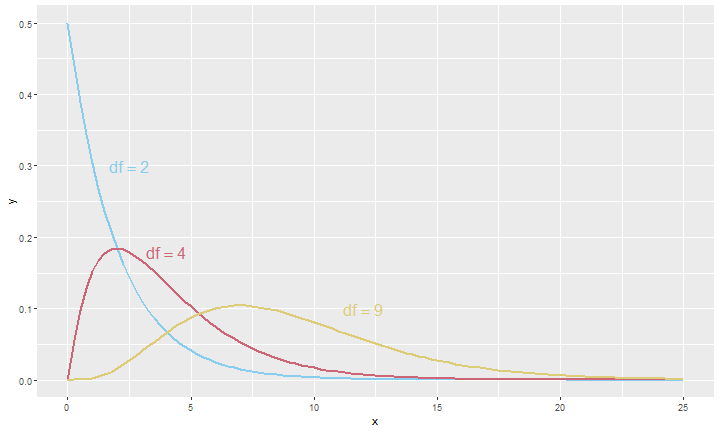
chi-Square Test Conditions

  • In order to use a chi-square distribution to compute a p-value, we need to check two conditions:

    • Independence. Each case that contributes a count to the table must be independent of all the other cases in the table.
10 / 23

chi-Square Test Conditions

  • In order to use a chi-square distribution to compute a p-value, we need to check two conditions:

    • Independence. Each case that contributes a count to the table must be independent of all the other cases in the table.

    • Sample size / distribution. Each particular scenario must have at least 5 expected cases.

10 / 23

chi-Square Test for One-Way Table

Suppose we are to evaluate whether there is convincing evidence that a set of observed counts O1, O2, …, Ok in k categories are unusually different from what we might expect under a null hypothesis. Denote the expected counts that are based on the null hypothesis by E1, E2, …, Ek. If each expected count is at least 5 and the null hypothesis is true, then the test statistic

X2=(O1−E1)2E1+(O2−E2)2E2+⋯+(Ok−Ek)2Ek follows a chi-square distribution with k−1 degrees of freedom. Note that this test statistic is always positive.

11 / 23

chi-Square Test for One-Way Table

Suppose we are to evaluate whether there is convincing evidence that a set of observed counts O1, O2, …, Ok in k categories are unusually different from what we might expect under a null hypothesis. Denote the expected counts that are based on the null hypothesis by E1, E2, …, Ek. If each expected count is at least 5 and the null hypothesis is true, then the test statistic

X2=(O1−E1)2E1+(O2−E2)2E2+⋯+(Ok−Ek)2Ek follows a chi-square distribution with k−1 degrees of freedom. Note that this test statistic is always positive.

The p-value for this test statistic is found by looking at the upper tail of this chi-square distribution. We consider the upper tail because larger values of X2 would provide greater evidence against the null hypothesis.

11 / 23

Example chi-Square Test

  • We expect the statistic for the one-way table for the jury data to follow a chi-square distribution with 3 degrees of freedom since there are k=4 categories.
12 / 23

Example chi-Square Test

  • We expect the statistic for the one-way table for the jury data to follow a chi-square distribution with 3 degrees of freedom since there are k=4 categories.

  • Then the probability of observing a value that is as or more extreme that the value obtained from the sample data is

1 - pchisq(5.89,3)
## [1] 0.1170863
12 / 23

Example chi-Square Test

  • We expect the statistic for the one-way table for the jury data to follow a chi-square distribution with 3 degrees of freedom since there are k=4 categories.

  • Then the probability of observing a value that is as or more extreme that the value obtained from the sample data is

1 - pchisq(5.89,3)
## [1] 0.1170863
  • Alternatively:
pchisq(5.89,3,lower.tail = FALSE)
## [1] 0.1170863
12 / 23

Example chi-Square Test

  • We expect the statistic for the one-way table for the jury data to follow a chi-square distribution with 3 degrees of freedom since there are k=4 categories.

  • Then the probability of observing a value that is as or more extreme that the value obtained from the sample data is

1 - pchisq(5.89,3)
## [1] 0.1170863
  • Alternatively:
pchisq(5.89,3,lower.tail = FALSE)
## [1] 0.1170863
  • We just computed a p-value, but to what null hypothesis does this p-value provide an appropriate means of testing?
12 / 23

Null Hypothesis for One-Way Tables

  • In our example, we would want to test:
13 / 23

Null Hypothesis for One-Way Tables

  • In our example, we would want to test:

    • H0: The jurors are a random sample, that is, there is no racial bias in who serves on a jury, and the observed counts reflect natural sampling fluctuation.
13 / 23

Null Hypothesis for One-Way Tables

  • In our example, we would want to test:

    • H0: The jurors are a random sample, that is, there is no racial bias in who serves on a jury, and the observed counts reflect natural sampling fluctuation.

    • HA: The jurors are not randomly sampled, that is, there is racial bias in juror selection.

13 / 23

Null Hypothesis for One-Way Tables

  • In our example, we would want to test:

    • H0: The jurors are a random sample, that is, there is no racial bias in who serves on a jury, and the observed counts reflect natural sampling fluctuation.

    • HA: The jurors are not randomly sampled, that is, there is racial bias in juror selection.

  • Using the data, we can conduct the chi-square test as follows:

chisq.test(c(26,25,205,19),p=c(0.07,0.12,0.72,0.09))
## 
##     Chi-squared test for given probabilities
## 
## data:  c(26, 25, 205, 19)
## X-squared = 5.8896, df = 3, p-value = 0.1171
13 / 23

More Examples

  • Let's see some more examples.
14 / 23

More Examples

  • Let's see some more examples.

  • Let's look at exercise 6.33 from the textbook on page 239. The table for the data will look as follows:

textbook purchased printed online total
Method 71.0 30.00 25.00 126
Expected percent 0.6 0.25 0.15 1
14 / 23

More Examples

  • Let's see some more examples.

  • Let's look at exercise 6.33 from the textbook on page 239. The table for the data will look as follows:

textbook purchased printed online total
Method 71.0 30.00 25.00 126
Expected percent 0.6 0.25 0.15 1
  • The expected counts will be
## purchased   printed    online 
##      75.6      31.5      18.9
14 / 23

More Examples

  • Let's see some more examples.

  • Let's look at exercise 6.33 from the textbook on page 239. The table for the data will look as follows:

textbook purchased printed online total
Method 71.0 30.00 25.00 126
Expected percent 0.6 0.25 0.15 1
  • The expected counts will be
## purchased   printed    online 
##      75.6      31.5      18.9
  • Thus, our X2 statistic is
(X2 <- (71-75.6)^2/75.6  + (30-31.5)^2/31.5  + (25-18.9)^2/18.9)
## [1] 2.320106
14 / 23

Example Continued

  • The appropriate degrees of freedom is 2. Therefore, the tail area is
pchisq(X2,2,lower.tail = FALSE)
## [1] 0.3134696
15 / 23

Example Continued

  • The appropriate degrees of freedom is 2. Therefore, the tail area is
pchisq(X2,2,lower.tail = FALSE)
## [1] 0.3134696
  • If our hypothesis is: H0: the distribution of the format of the book used follows the expected distribution, vs. HA: the distribution of the format of the book used does not follow the expected distribution, then we will fail to reject the null hypothesis at the α=0.05 level of significance.
15 / 23

Example Continued

  • The appropriate degrees of freedom is 2. Therefore, the tail area is
pchisq(X2,2,lower.tail = FALSE)
## [1] 0.3134696

  • If our hypothesis is: H0: the distribution of the format of the book used follows the expected distribution, vs. HA: the distribution of the format of the book used does not follow the expected distribution, then we will fail to reject the null hypothesis at the α=0.05 level of significance.

  • We can confirm our result using R:

chisq.test(c(71,30,25),p=c(0.6,0.25,0.15))
## 
##     Chi-squared test for given probabilities
## 
## data:  c(71, 30, 25)
## X-squared = 2.3201, df = 2, p-value = 0.3135
15 / 23

Two-Way Tables

  • A one-way table describes counts for each outcome in a single categorical variable.
16 / 23

Two-Way Tables

  • A one-way table describes counts for each outcome in a single categorical variable.

  • A two-way table describes counts for combinations of two categorical variables where at least one of the two has more than 2 levels.

16 / 23

Two-Way Tables

  • A one-way table describes counts for each outcome in a single categorical variable.

  • A two-way table describes counts for combinations of two categorical variables where at least one of the two has more than 2 levels.

  • When we consider a two-way table, we often would like to know, are these variables related in any way? That is, are they dependent versus independent?

16 / 23

Null Hypothesis for Two-Way Tables

  • For a two-way table problem, the typical hypotheses are of the form
17 / 23

Null Hypothesis for Two-Way Tables

  • For a two-way table problem, the typical hypotheses are of the form

    • H0: The two variables are independent.
17 / 23

Null Hypothesis for Two-Way Tables

  • For a two-way table problem, the typical hypotheses are of the form

    • H0: The two variables are independent.

    • HA: The two variables are dependent.

17 / 23

Null Hypothesis for Two-Way Tables

  • For a two-way table problem, the typical hypotheses are of the form

    • H0: The two variables are independent.

    • HA: The two variables are dependent.

  • Let's look at an example.

17 / 23

Offshore Drilling Example

  • Consider the data with first few rows shown below:
## # A tibble: 6 x 2
##   position college_grad
##   <fct>    <fct>       
## 1 support  yes         
## 2 support  yes         
## 3 support  yes         
## 4 support  yes         
## 5 support  yes         
## 6 support  yes
18 / 23

Offshore Drilling Example

  • Consider the data with first few rows shown below:
## # A tibble: 6 x 2
##   position college_grad
##   <fct>    <fct>       
## 1 support  yes         
## 2 support  yes         
## 3 support  yes         
## 4 support  yes         
## 5 support  yes         
## 6 support  yes
  • Let's look at the corresponding two-way table:
addmargins(table(my_offshore_drilling$position,my_offshore_drilling$college_grad))
##              
##                no yes Sum
##   do_not_know 131 104 235
##   oppose      126 180 306
##   support     132 154 286
##   Sum         389 438 827
18 / 23

Hypothesis Test for Offshore Drilling

  • We would like to test the hypothesis:
19 / 23

Hypothesis Test for Offshore Drilling

  • We would like to test the hypothesis:

    • H0: College graduate status and support for offshore drilling are independent.
19 / 23

Hypothesis Test for Offshore Drilling

  • We would like to test the hypothesis:

    • H0: College graduate status and support for offshore drilling are independent.

    • HA: College graduate status and support for offshore drilling are not independent.

19 / 23

Hypothesis Test for Offshore Drilling

  • We would like to test the hypothesis:

    • H0: College graduate status and support for offshore drilling are independent.

    • HA: College graduate status and support for offshore drilling are not independent.

  • This is easily done with

chisq.test(my_offshore_drilling$position,my_offshore_drilling$college_grad)
## 
##     Pearson's Chi-squared test
## 
## data:  my_offshore_drilling$position and my_offshore_drilling$college_grad
## X-squared = 11.461, df = 2, p-value = 0.003246
19 / 23

Hypothesis Test for Offshore Drilling

  • We would like to test the hypothesis:

    • H0: College graduate status and support for offshore drilling are independent.

    • HA: College graduate status and support for offshore drilling are not independent.

  • This is easily done with

chisq.test(my_offshore_drilling$position,my_offshore_drilling$college_grad)
## 
##     Pearson's Chi-squared test
## 
## data:  my_offshore_drilling$position and my_offshore_drilling$college_grad
## X-squared = 11.461, df = 2, p-value = 0.003246
  • Thus, we will reject the null hypothesis at the α=0.05 significance level.
19 / 23

Tests By Hand

  • Let's see how to conduct the previous test by hand.
20 / 23

Tests By Hand

  • Let's see how to conduct the previous test by hand.

  • The two things we need to know are the value of the X2 statistic and the appropriate number of degrees of freedom to use.

20 / 23

Tests By Hand

  • Let's see how to conduct the previous test by hand.

  • The two things we need to know are the value of the X2 statistic and the appropriate number of degrees of freedom to use.

  • When applying the chi-square test to a two-way table, we use

df=(R−1)×(C−1)

where R is the number of rows in the table and C is the number of columns.

20 / 23

Tests By Hand

  • Let's see how to conduct the previous test by hand.

  • The two things we need to know are the value of the X2 statistic and the appropriate number of degrees of freedom to use.

  • When applying the chi-square test to a two-way table, we use

df=(R−1)×(C−1)

where R is the number of rows in the table and C is the number of columns.

  • Thus, in our example, df=(3−1)×(2−1)=2.
20 / 23

Computing X2

  • As before

X2=∑(O−E)2E

21 / 23

Computing X2

  • As before

X2=∑(O−E)2E

  • The question is, how do we compute the expected counts ( Eij ) for a two-way table? The answer is

Expected Countrow i col j=Eij=row i total×column j totaltable total

21 / 23

Computing X2

  • As before

X2=∑(O−E)2E

  • The question is, how do we compute the expected counts ( Eij ) for a two-way table? The answer is

Expected Countrow i col j=Eij=row i total×column j totaltable total

  • Let's work this out on the board for our example.
21 / 23

Hypothesis Testing Summary

  • To date, we have covered the following tests:
22 / 23

Hypothesis Testing Summary

  • To date, we have covered the following tests:

    • Single proportion and difference of proportions using a "z-test."
22 / 23

Hypothesis Testing Summary

  • To date, we have covered the following tests:

    • Single proportion and difference of proportions using a "z-test."

    • Single mean, paired mean, difference of means using a "t-test."

22 / 23

Hypothesis Testing Summary

  • To date, we have covered the following tests:

    • Single proportion and difference of proportions using a "z-test."

    • Single mean, paired mean, difference of means using a "t-test."

    • Comparing many means with ANOVA.

22 / 23

Hypothesis Testing Summary

  • To date, we have covered the following tests:

    • Single proportion and difference of proportions using a "z-test."

    • Single mean, paired mean, difference of means using a "t-test."

    • Comparing many means with ANOVA.

    • One-way and two-way table tests for categorical variables with chi-square.

22 / 23

Hypothesis Testing Summary

  • To date, we have covered the following tests:

    • Single proportion and difference of proportions using a "z-test."

    • Single mean, paired mean, difference of means using a "t-test."

    • Comparing many means with ANOVA.

    • One-way and two-way table tests for categorical variables with chi-square.

    • Simple linear regression via ordinary least squares for a pair of numeric variable.

22 / 23

Hypothesis Testing Summary

  • To date, we have covered the following tests:

    • Single proportion and difference of proportions using a "z-test."

    • Single mean, paired mean, difference of means using a "t-test."

    • Comparing many means with ANOVA.

    • One-way and two-way table tests for categorical variables with chi-square.

    • Simple linear regression via ordinary least squares for a pair of numeric variable.

  • We also know how to construct confidence intervals for parameter estimates for proportions, difference of proportions, mean, difference of means, and intercept and slope parameters for a linear model.

22 / 23

Next Topic

  • Our next topic discusses more regarding regression. This video will get you started:
23 / 23

Inference for Categorical Data

In this lecture, we will examine two new inferential techniques:

2 / 23
Paused

Help

Keyboard shortcuts

↑, ←, Pg Up, k Go to previous slide
↓, →, Pg Dn, Space, j Go to next slide
Home Go to first slide
End Go to last slide
Number + Return Go to specific slide
b / m / f Toggle blackout / mirrored / fullscreen mode
c Clone slideshow
p Toggle presenter mode
t Restart the presentation timer
?, h Toggle this help
Esc Back to slideshow