Lecture 12

class: center, middle, inverse, title-slide

# Lecture 12
### JMG
### MATH 204

---

# Multiple Regression

- Multiple regression builds on the foundations of simple linear regression to allow for more than one predictor. Watch the following video to get started.

---

# Learning Objectives

- After this lecture, you should

- know how to fit a multiple regression model using `lm`,
  
--

- understand and be able to interpret adjusted `$R^2$`, and 
  
--

- be able to use diagnostic plots to assess the validity of a linear fit. 
  
---

# Motivating Data

- Consider the `mariokart` data set which consists of auction data from Ebay for the game Mario Kart for the Nintendo Wii. This data was collected in early October 2009.

```r
head(mariokart)
```

```
## # A tibble: 6 x 12
##          id duration n_bids cond  start_pr ship_pr total_pr ship_sp  seller_rate
##       <dbl>    <int>  <int> <fct>    <dbl>   <dbl>    <dbl> <fct>          <int>
## 1   1.50e11        3     20 new       0.99    4        51.6 standard        1580
## 2   2.60e11        7     13 used      0.99    3.99     37.0 firstCl~         365
## 3   3.20e11        3     16 new       0.99    3.5      45.5 firstCl~         998
## 4   2.80e11        3     18 new       0.99    0        44   standard           7
## 5   1.70e11        1     20 new       0.01    0        71   media            820
## 6   3.60e11        3     19 new       0.99    4        45   standard      270144
## # ... with 3 more variables: stock_photo <fct>, wheels <int>, title <fct>
```

- Let's obtain another view of this data.

---

# Glimpse of `mariokart`

```r
glimpse(mariokart)
```

```
## Rows: 141
## Columns: 12
## $ id          <dbl> 150377422259, 260483376854, 320432342985, 280405224677, 17~
## $ duration    <int> 3, 7, 3, 3, 1, 3, 1, 1, 3, 7, 1, 1, 1, 1, 7, 7, 3, 3, 1, 1~
## $ n_bids      <int> 20, 13, 16, 18, 20, 19, 13, 15, 29, 8, 15, 15, 13, 16, 6, ~
## $ cond        <fct> new, used, new, new, new, new, used, new, used, used, new,~
## $ start_pr    <dbl> 0.99, 0.99, 0.99, 0.99, 0.01, 0.99, 0.01, 1.00, 0.99, 19.9~
## $ ship_pr     <dbl> 4.00, 3.99, 3.50, 0.00, 0.00, 4.00, 0.00, 2.99, 4.00, 4.00~
## $ total_pr    <dbl> 51.55, 37.04, 45.50, 44.00, 71.00, 45.00, 37.02, 53.99, 47~
## $ ship_sp     <fct> standard, firstClass, firstClass, standard, media, standar~
## $ seller_rate <int> 1580, 365, 998, 7, 820, 270144, 7284, 4858, 27, 201, 4858,~
## $ stock_photo <fct> yes, yes, no, yes, yes, yes, yes, yes, yes, no, yes, yes, ~
## $ wheels      <int> 1, 1, 1, 1, 2, 0, 0, 2, 1, 1, 2, 2, 2, 2, 1, 0, 1, 1, 2, 0~
## $ title       <fct> "~~ Wii MARIO KART &amp; WHEEL ~ NINTENDO Wii ~ BRAND NEW ~
```

- **Question:** What features affect the final price (`total_pr`) at which a game is sold?

---

# A First Model

- As a start, we fit a linear model with the game condition (`cond`) as the only predictor:

```r
lm_fit <- lm(total_pr~cond,data=mariokart)
summary(lm_fit)
```

```
## 
## Call:
## lm(formula = total_pr ~ cond, data = mariokart)
## 
## Residuals:
##      Min       1Q   Median       3Q      Max 
## -13.8911  -5.8311   0.1289   4.1289  22.1489 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept)  53.7707     0.9596  56.034  < 2e-16 ***
## condused    -10.8996     1.2583  -8.662 1.06e-14 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 7.371 on 139 degrees of freedom
## Multiple R-squared:  0.3506,	Adjusted R-squared:  0.3459 
## F-statistic: 75.03 on 1 and 139 DF,  p-value: 1.056e-14
```

---

# Results

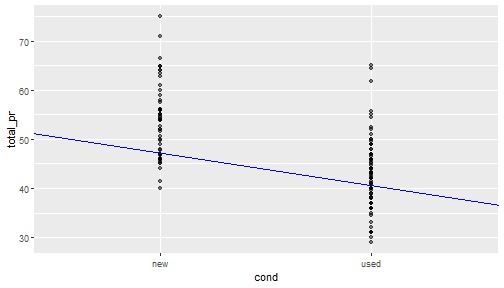
- Our first fit predicts that a used game will, on average, go for $10.90 less than a new game will.

![](lect_12_files/figure-html/unnamed-chunk-5-1.png)

- **Question:** Do you think that the condition of the game alone is sufficient to predict the price of the game? Explain why or why not.

---

# Adding Predictors

- As we will see, in R it is extremely easy to fit a model with many predictors. Why might we want to do this?

- We would like to fit a model that includes all potentially important variables simultaneously.

- Multiple regression can help us evaluate the relationship between a predictor variable and the outcome while controlling for the potential influence of other variables.

- Let's fit a more complicated linear model.

---

# Multiple Regression Model

- A multiple regression model is a linear model with many predictors. In general, we write the model as

`$$\hat{y} = \beta_{0} + \beta_{1}x_{1} + \beta_{2}x_{2} + \cdots + \beta_{k}x_{k}$$`

when there are `$k$` predictors. We always estimate the `$\beta_{i}$` parameters using statistical software.

- For example, we may want to use `cond`, `stock_photo` (whether the auction feature photo was a stock photo or not), `duration` (auction length, in days), and `wheels` (number of Wii wheels included in the auction) all as predictors of price for the `mariokart` data.

- Let's obtain a linear fit with these predictors using `lm`.

---

# Another Fit

```r
lm_fit2 <- lm(total_pr~cond+stock_photo+duration+wheels,data=mariokart)
summary(lm_fit2)
```

```
## 
## Call:
## lm(formula = total_pr ~ cond + stock_photo + duration + wheels, 
##     data = mariokart)
## 
## Residuals:
##      Min       1Q   Median       3Q      Max 
## -11.3788  -2.9854  -0.9654   2.6915  14.0346 
## 
## Coefficients:
##                Estimate Std. Error t value Pr(>|t|)    
## (Intercept)    41.34153    1.71167  24.153  < 2e-16 ***
## condused       -5.13056    1.05112  -4.881 2.91e-06 ***
## stock_photoyes  1.08031    1.05682   1.022    0.308    
## duration       -0.02681    0.19041  -0.141    0.888    
## wheels          7.28518    0.55469  13.134  < 2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 4.901 on 136 degrees of freedom
## Multiple R-squared:  0.719,	Adjusted R-squared:  0.7108 
## F-statistic: 87.01 on 4 and 136 DF,  p-value: < 2.2e-16
```

---

# Results

- Notice that when we have controlled for other features, the condition (new versus used) of the game  has a smaller impact on the price of the game since the slope estimate has gone from -10.90 to -5.13.

- For simple linear regression, we used `$R^2$` to determine the amount of variability in the response that was explained by the model. Recall that

`$$R^2 = 1 - \frac{\text{variability in residuals}}{\text{variability in the response}}$$`

- `$R^2$` does not work well for mulitple regression. Instead, we use **adjusted** `$R^2$`.

---

# Adjusted `$R^2$`

- The adjusted `$R^2$` is computed as

`$$R^2_{\text{adj}} = 1 - \frac{s_{\text{residuals}}^{2}}{s_{\text{response}}^{2}}\frac{n-1}{n-k-1}$$`
where `$n$` is the number of observations and `$k$` is the number of predictor variables. Remember that a categorical predictor with `$p$` levels will contribute `$p-1$` to the number of variables in the model.

- Notice that the adjusted `$R^2$` will be smaller than the unadjusted `$R^2$`.

- One of the main benefits of using adjusted `$R^2$` for multiple regression is that it accounts for **model complexity**.

- The best model is not always the most complicated one. For one, more complex models are more likely to overfit.

---

# Model Selection

- Model selection seeks to identify variables in the model that may not be helpful.

- The model that includes all available explanatory variables is referred to as the full model.

- There are a variety of model selection strategies that are used in practice. We will discuss two of the more common approaches.

---

# Model Selecion Video

- This video provides further perspective on model selection.

---

# Model Selection Strategies

- **Backward Elimination**. In this approach, we would identify the predictor corresponding to the largest `$p$`-value. If the `$p$`-value is above the significance level (usually `$\alpha=0.05$`), then we drop that variable, refit the model, and repeat the process. If the largest `$p$`-value is less than the significance level, then we would not eliminate any predictors.

- **Forward Selection**. This approach begins with no predictors, then we fit a model with each individual predictor one at a time and keep the predictor that has the smallest `$p$`-value. Forward selection proceeds by continuing to add at each step a predictor that results in the smallest `$p$`-value that is less than the significance level. When none of the remaining predictors can be added to the model and have a `$p$`-value less than the significance level, we stop.

- It is important to note that backward elimination and forward selection may not produce the same final model.

---

# Model Selection Example

- Let's see both backward elimination and forward selection applied to the `mariokart` data. Note that the full model is (in R formula notation) `total_pr ~ cond + stock_photo + duration + wheels`.

- Let's work out the details together in R.

- Backward elimination and forward selection use `$p$`-values in deciding which variables will make up the final model. However, there are other measures that are used in other approaches to model selection. For example, one could seek a model that has the largest adjusted `$R^2$` value. Information theoretic measures such as [AIC](https://en.wikipedia.org/wiki/Akaike_information_criterion) and [BIC](https://en.wikipedia.org/wiki/Bayesian_information_criterion) are also often used. A discussion on these matters falls outside the scope of this course.

- We note that there are packages associated with statistical software that implement various variable selection algorithms. For example, [`olsrr`](https://olsrr.rsquaredacademy.com/) is an R package that implements a variety of variable selection methods.

---

# Checking Model Conditions

- Multiple regression methods using the model

`$$\hat{y} = \beta_{0} + \beta_{1}x_{1} + \beta_{2}x_{2} + \cdots + \beta_{k}x_{k}$$`
generally depend on the following four conditions:

- the residuals of the model are nearly normal,
  
--

- the variability of the residuals is nearly constant,
  
--

- the residuals are independent, and
  
--

- each variable is linearly related to the response. 
  
--

- Diagnostic plots can be used to check each of these conditions.

---

# Histogram of Residuals

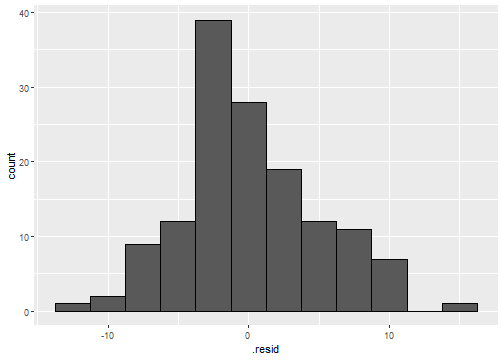
- A histogram of the residuals can be used to check for outliers. For example, the residuals for the final model for the `mariokart` data have the following histogram:

![](lect_12_files/figure-html/unnamed-chunk-8-1.png)

- There are no extreme outliers present.

---

# Absolute Value of Residuals

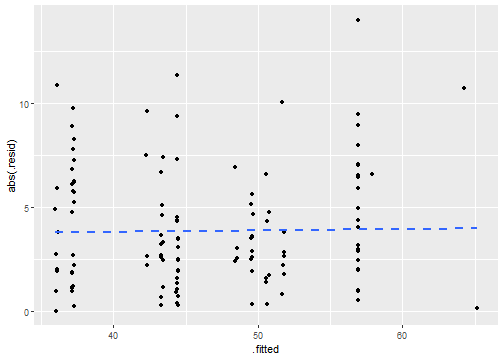
- A plot of the absolute value of residuals versus fitted values is helpful to check the condition that the variance of residuals is approximately constant.

![](lect_12_files/figure-html/unnamed-chunk-9-1.png)

- There is no evident distinguished pattern.

---

# Additional Diagnostic Plots

- It can also be useful to examine the following types of plots:

- Residuals in the order of their data collection. Such a plot is helpful in identifying any connection between cases that are close to one another. 
  
--

- Residuals against each predictor. We are looking for any notable change in variability between groups. 
  
--

- These plots are shown for model results for the `mariokart` data on pages 369 and 370 of the textbook. Let's look at these together and discuss.

---

# Diagnostic Plots Video

- Watch the following video for further perspective on assessing multiple regression with plots.

---

# Further Regression

- When it comes to regression, we have only scratched the surface. There is more we could discuss regarding multiple regression, and there are also other types of regression.  The following video provides an introduction to logistic regression
<div class="vembedr" align="center">
<div>
<iframe src="https://www.youtube.com/embed/uYC2eLVSpI8" width="533" height="300" frameborder="0" allowfullscreen=""></iframe>
</div>
</div>

- For even more on regression, we recommend the text [Linear Models with R](https://julianfaraway.github.io/faraway/LMR/) by Faraway.